
【題目】如圖,已知四棱錐P-ABCD中,底面ABCD是直角梯形,AD//BC,BC=2AD,AD⊥CD,PD⊥平面ABCD,E為PB的中點(diǎn).
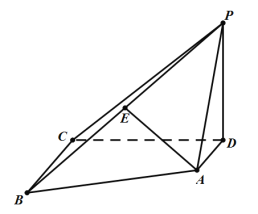
(1)求證:AE//平面PDC;
(2)若BC=CD=PD,求直線AC與平面PBC所成角的余弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連結(jié)
,連結(jié)![]() 、
、![]() ,推導(dǎo)出四邊形
,推導(dǎo)出四邊形![]() 是平行四邊形,從而
是平行四邊形,從而![]() ,由此能證明
,由此能證明![]() 平面
平面![]() .
.
(2)推導(dǎo)出![]() ,由
,由![]() ,得
,得![]() ,再推導(dǎo)出
,再推導(dǎo)出![]() ,
,![]() ,從而
,從而![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,進(jìn)而
,進(jìn)而![]() 平面
平面![]() ,連結(jié)
,連結(jié)![]() ,
,![]() ,則
,則![]() 就是直線
就是直線![]() 與平面
與平面![]() 所成角,由此能求出直線
所成角,由此能求出直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
解:(1)證明:取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連結(jié)
,連結(jié)![]() 、
、![]() ,
,
![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
![]() 四邊形
四邊形![]() 是平行四邊形,
是平行四邊形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
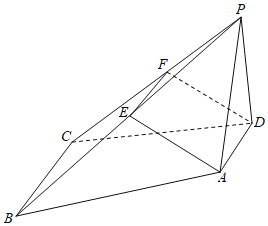
(2)解:![]() ,
,![]() 是等腰三角形,
是等腰三角形,
![]() ,又
,又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
連結(jié)![]() ,
,![]() ,則
,則![]() 就是直線
就是直線![]() 與平面
與平面![]() 所成角,
所成角,
設(shè)![]() ,
,
在![]() 中,解得
中,解得![]() ,
,![]() ,
,![]() ,
,
在![]() 中,解得
中,解得![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() 直線
直線![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為![]() .
.


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個(gè)盒子里裝有![]() 個(gè)均勻的紅球和
個(gè)均勻的紅球和![]() 個(gè)均勻的白球,每個(gè)球被取到的概率相等,已知從盒子里一次隨機(jī)取出1個(gè)球,取到的球是紅球的概率為
個(gè)均勻的白球,每個(gè)球被取到的概率相等,已知從盒子里一次隨機(jī)取出1個(gè)球,取到的球是紅球的概率為![]() ,從盒子里一次隨機(jī)取出2個(gè)球,取到的球至少有1個(gè)是白球的概率為
,從盒子里一次隨機(jī)取出2個(gè)球,取到的球至少有1個(gè)是白球的概率為![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若一次從盒子里隨機(jī)取出3個(gè)球,求取到的白球個(gè)數(shù)不小于紅球個(gè)數(shù)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市一所醫(yī)院在某時(shí)間段為發(fā)燒超過38![]() 的病人特設(shè)發(fā)熱門診,該門診記錄了連續(xù)5天晝夜溫差
的病人特設(shè)發(fā)熱門診,該門診記錄了連續(xù)5天晝夜溫差![]() (
(![]() )與就診人數(shù)
)與就診人數(shù)![]() 的資料:
的資料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
晝夜溫差 | 8 | 10 | 13 | 12 | 7 |
就診人數(shù) | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相關(guān)系數(shù)
的相關(guān)系數(shù)![]() ,并說明晝夜溫差(
,并說明晝夜溫差(![]() )與就診人數(shù)
)與就診人數(shù)![]() 具有很強(qiáng)的線性相關(guān)關(guān)系.
具有很強(qiáng)的線性相關(guān)關(guān)系.
(2)求就診人數(shù)![]() (人)關(guān)于出晝夜溫差
(人)關(guān)于出晝夜溫差![]() (
(![]() )的線性回歸方程,預(yù)測(cè)晝夜溫差為9
)的線性回歸方程,預(yù)測(cè)晝夜溫差為9![]() 時(shí)的就診人數(shù).
時(shí)的就診人數(shù).
附:樣本![]()
![]() 的相關(guān)系數(shù)為
的相關(guān)系數(shù)為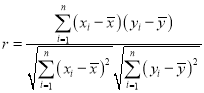 ,當(dāng)
,當(dāng)![]() 時(shí)認(rèn)為兩個(gè)變量有很強(qiáng)的線性相關(guān)關(guān)系.
時(shí)認(rèn)為兩個(gè)變量有很強(qiáng)的線性相關(guān)關(guān)系.
回歸直線方程為![]() ,其中
,其中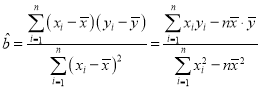 ,
,![]() .
.
參考數(shù)據(jù):![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定點(diǎn)![]() ,
,![]() ,直線
,直線![]() 、
、![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動(dòng)點(diǎn)
,記動(dòng)點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() 。
。
(1)求曲線![]() 的方程;
的方程;
(2)過點(diǎn)![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點(diǎn),是否存在定點(diǎn)
兩點(diǎn),是否存在定點(diǎn)![]() ,使得直線
,使得直線![]() 與
與![]() 斜率之積為定值,若存在,求出
斜率之積為定值,若存在,求出![]() 坐標(biāo);若不存在,請(qǐng)說明理由。
坐標(biāo);若不存在,請(qǐng)說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 市某機(jī)構(gòu)為了調(diào)查該市市民對(duì)我國(guó)申辦
市某機(jī)構(gòu)為了調(diào)查該市市民對(duì)我國(guó)申辦![]() 年足球世界杯的態(tài)度,隨機(jī)選取了
年足球世界杯的態(tài)度,隨機(jī)選取了![]() 位市民進(jìn)行調(diào)查,調(diào)查結(jié)果統(tǒng)計(jì)如下:
位市民進(jìn)行調(diào)查,調(diào)查結(jié)果統(tǒng)計(jì)如下:
支持 | 不支持 | 合計(jì) | |
男性市民 |
| ||
女性市民 |
| ||
合計(jì) |
|
|
(1)根據(jù)已知數(shù)據(jù),把表格數(shù)據(jù)填寫完整;
(2)利用(1)完成的表格數(shù)據(jù)回答下列問題:
(i)能否在犯錯(cuò)誤的概率不超過![]() 的前提下認(rèn)為支持申辦足球世界杯與性別有關(guān);
的前提下認(rèn)為支持申辦足球世界杯與性別有關(guān);
(ii)已知在被調(diào)查的支持申辦足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教師,現(xiàn)從這
位是教師,現(xiàn)從這![]() 位退休老人中隨機(jī)抽取
位退休老人中隨機(jī)抽取![]() 人,求至多有
人,求至多有![]() 位老師的概率.
位老師的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,AC⊥BC,且,AC=BC=2,D,E分別為AB,PB中點(diǎn),PD⊥平面ABC,PD=3.
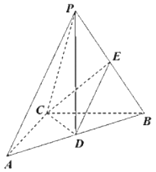
(1)求直線CE與直線PA夾角的余弦值;
(2)求直線PC與平面DEC夾角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市一所醫(yī)院在某時(shí)間段為發(fā)燒超過38![]() 的病人特設(shè)發(fā)熱門診,該門診記錄了連續(xù)5天晝夜溫差
的病人特設(shè)發(fā)熱門診,該門診記錄了連續(xù)5天晝夜溫差![]() (
(![]() )與就診人數(shù)
)與就診人數(shù)![]() 的資料:
的資料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
晝夜溫差 | 8 | 10 | 13 | 12 | 7 |
就診人數(shù) | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相關(guān)系數(shù)
的相關(guān)系數(shù)![]() ,并說明晝夜溫差(
,并說明晝夜溫差(![]() )與就診人數(shù)
)與就診人數(shù)![]() 具有很強(qiáng)的線性相關(guān)關(guān)系.
具有很強(qiáng)的線性相關(guān)關(guān)系.
(2)求就診人數(shù)![]() (人)關(guān)于出晝夜溫差
(人)關(guān)于出晝夜溫差![]() (
(![]() )的線性回歸方程,預(yù)測(cè)晝夜溫差為9
)的線性回歸方程,預(yù)測(cè)晝夜溫差為9![]() 時(shí)的就診人數(shù).
時(shí)的就診人數(shù).
附:樣本![]()
![]() 的相關(guān)系數(shù)為
的相關(guān)系數(shù)為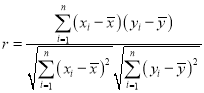 ,當(dāng)
,當(dāng)![]() 時(shí)認(rèn)為兩個(gè)變量有很強(qiáng)的線性相關(guān)關(guān)系.
時(shí)認(rèn)為兩個(gè)變量有很強(qiáng)的線性相關(guān)關(guān)系.
回歸直線方程為![]() ,其中
,其中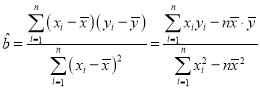 ,
,![]() .
.
參考數(shù)據(jù):![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,在點(diǎn)
,在點(diǎn)![]() 處的切線方程為
處的切線方程為![]() ,求(1)實(shí)數(shù)
,求(1)實(shí)數(shù)![]() 的值;(2)函數(shù)
的值;(2)函數(shù)![]() 的單調(diào)區(qū)間以及在區(qū)間
的單調(diào)區(qū)間以及在區(qū)間![]() 上的最值.
上的最值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com