
【題目】如圖,在矩形ABCD中,AB=6,BC=4,動點Q在邊AB上,連接CQ,將△BQC沿CQ所在的直線對折得到△CQN,延長QN交直線CD于點M.
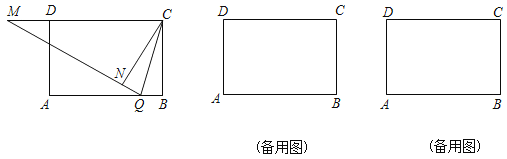
(1)求證:MC=MQ
(2)當BQ=1時,求DM的長;
(3)過點D作DE⊥CQ,垂足為點E,直線QN與直線DE交于點F,且![]() ,求BQ的長.
,求BQ的長.
【答案】(1)見解析;(2)2.5;(3)![]() 或2
或2
【解析】
(1)由矩形的性質得出∠B=90°,AB=CD=6,CD∥AB,得出∠MCQ=∠CQB,由折疊的性質得出△CBQ≌△CNQ,求出BC=NC=4,NQ=BQ=1,∠CNQ=∠B=90°,∠CQN=∠CQB,得出∠CNM=90°,∠MCQ=∠CQN,證出MC=MQ.
(2)設DM=x,則MQ=MC=6+x,MN=5+x,在Rt△CNM中,由勾股定理得出方程,解方程即可.
(3)分兩種情況:①當點M在CD延長線上時,由(1)得:∠MCQ=∠CQM,證出∠FDM=∠F,得出MD=MF,過M作MH⊥DF于H,則DF=2DH,證明△MHD∽△CED,得出![]() ,求出MD=
,求出MD=![]() CD=1,MC=MQ=7,由勾股定理得出MN即可解決問題.
CD=1,MC=MQ=7,由勾股定理得出MN即可解決問題.
②當點M在CD邊上時,同①得出BQ=2即可.
(1)證明:∵四邊形ABCD是矩形,
∴DC∥AB
即∠MCQ=∠CQB,
∵△BQC沿CQ所在的直線對折得到△CQN,
∴∠CQN=∠CQB,
即∠MCQ=∠MQC,
∴MC=MQ.
(2)∵四邊形ABCD是矩形,△BQC沿CQ所在的直線對折得到△CQN,
∴∠CNM=∠B=90°,
設DM=x,則MQ=MC=6+x,MN=5+x,
在Rt△CNM中,MB2=BN2+MN2,
即(x+6)2=42+(x+5)2,
解得:x=![]() ,
,
∴DM=![]() ,
,
∴DM的長2.5.
(3)解:分兩種情況:
①當點M在CD延長線上時,如圖所示: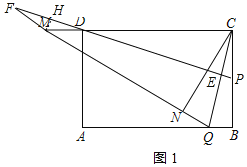
由(1)得∠MCQ=∠MQC,
∵DE⊥CQ,
∴∠CDE=∠F,
又∵∠CDE=∠FDM,
∴∠FDM=∠F,
∴MD=MF.
過M點作MH⊥DF于H,則DF=2DH,
又![]() ,
,
∴![]() ,
,
∵DE⊥CQMH⊥DF,
∴∠MHD=∠DEC=90°,
∴△MHD∽△DEC
∴![]() ,
,
∴DM=1,MC=MQ=7,
∴MN=![]()
∴BQ=NQ=![]()
②當點M在CD邊上時,如圖所示,類似可求得BQ=2.
綜上所述,BQ的長為![]() 或2.
或2.


 巧學巧練系列答案
巧學巧練系列答案科目:初中數學 來源: 題型:
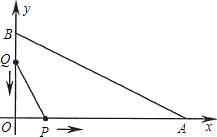
【題目】在平面直角坐標系中,已知OA=10cm,OB=5cm,點P從點O開始沿OA邊向點A以2cm/s的速度移動;點Q從點B開始沿BO邊向點O以1cm/s的速度移動.如果P、Q同時出發,用t(s)表示移動的時間(0≤t≤5),
(1)用含t的代數式表示:線段PO= cm;OQ= cm.
(2)當t為何值時,四邊形PABQ的面積為19cm2.
(3)當△POQ與△AOB相似時,求出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一副三角板如圖①放置,其中![]() ,斜邊
,斜邊![]() ,把三角板
,把三角板![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,得到
,得到![]() ,如圖②,這時
,如圖②,這時![]() 與
與![]() 相交于點
相交于點![]() ,與
,與![]() 相交于點
相交于點![]() .
.
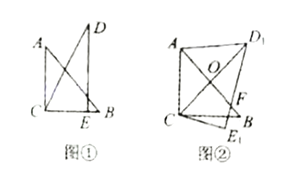
(1)求![]() 的度數;
的度數;
(2)求線段![]() 的長;
的長;
(3)若把![]() 繞著點
繞著點![]() 順時針再旋轉
順時針再旋轉![]() ,得
,得![]() .這時點
.這時點![]() 在
在![]() 的內部、外部,還是邊上?請說明理由,
的內部、外部,還是邊上?請說明理由,
查看答案和解析>>
科目:初中數學 來源: 題型:
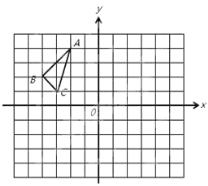
【題目】△ABC 在平面直角坐標系中的位置如圖所示,其中每 個小正方形的邊長為 1 個單位長度.
(1)畫出△ABC 關于原點 O 的中心對稱圖形△A1B1C1,并寫出點 A1 的坐標;
(2)將△ABC 繞點 C 順時針旋轉 90°得到△A2B2C,畫出△A2B2C,求在旋轉過程中,點 A 所經過的路徑長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程M為ax2+bx+c=0、N為cx2+bx+a=0(a≠c),則下列結論:①如果5是方程M的一個根,那么![]() 是方程N的一個根;②如果方程M有兩個不相等的實數根,那么方程N也有兩個不相等的實數根;③如果方程M與方程N有一個相同的根,那么這個根必是x=1.其中正確的結論是( )
是方程N的一個根;②如果方程M有兩個不相等的實數根,那么方程N也有兩個不相等的實數根;③如果方程M與方程N有一個相同的根,那么這個根必是x=1.其中正確的結論是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
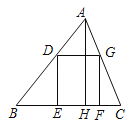
【題目】如圖,四邊形DEFG是△ABC的內接正方形,D、G分別在AB、AC上,E、F在BC上,AH是△ABC的高,已知BC=20,AH=16,求正方形DEFG的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣4x+3.
(1)用配方法將y=x2﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)在平面直角坐標系中,畫出這個二次函數的圖象;
(3)寫出當x為何值時,y>0.
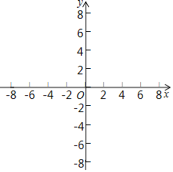
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,∠A=30°,點D是AB的中點,DE⊥BC,垂足為點E,連接CD.
(1)如圖1,DE與BC的數量關系是 ;
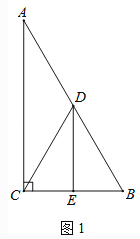
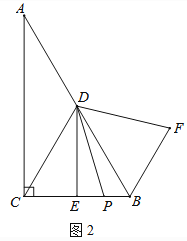
(2)如圖2,若P是線段CB上一動點(點P不與點B、C重合),連接DP,將線段DP繞點D逆時針旋轉60°,得到線段DF,連接BF,請猜想DE、BF、BP三者之間的數量關系,并證明你的結論;
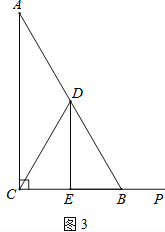
(3)若點P是線段CB延長線上一動點,按照(2)中的作法,請在圖3中補全圖形,并直接寫出DE、BF、BP三者之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程kx2﹣3x+1=0有實數根.
(1)求k的取值范圍;
(2)若該方程有兩個實數根,分別為x1和x2,當x1+x2+x1x2=4時,求k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com