
如圖,點![]() 是等邊
是等邊![]() 內(nèi)一點,
內(nèi)一點,![]() .將
.將![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得
得![]() ,連接
,連接![]()
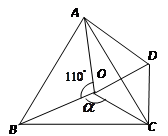
1.求證: ![]() 是等邊三角形;
是等邊三角形;
2.當![]() 時,試判斷
時,試判斷![]() 的形狀,并說明理由
的形狀,并說明理由
3.探究:當![]() 為多少度時,
為多少度時,![]() 是等腰三角形?
是等腰三角形?
1.證明:∵OC=OD, ∠OCD=60°,∴ △COD是等邊三角形。…………(2分)
2.當α=150°時, △AOD是Rt△。理由如下:………………………………(3分)
∵△COD為等邊三角形,∴ ∠COD=∠CDO=60°
又∠ADC=α=150° ∴ ∠ADO=90°
3.∵∠COD=∠CDO=60° ∠ADO=α-60°
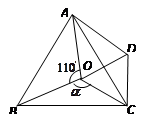
∴ ∠AOD=360°-110°-60°-α=190°-α
∴∠OAD=180°-(190°-α)-(α-60°)=50°
① 若 190°-α=α-60° ∴ α=125°
② 若 190°-α=50° ∴ α=140°
③ 若α-60°=50° ∴ α=110°
故 當α=125°或140°或110°時,△AOD是等腰三角形。
解析:略


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:
如圖,點是等邊
內(nèi)一點,
,
.將
繞點
按順時針方向旋轉
得
,連接
.

(1)當,
時,試判斷
的形狀,并說明理由。
(2)探究:若,那么
為多少度,
是等腰三角形?
(只要寫出探究結果)= 。
(3)請寫出是等邊三角形時
、
的度數(shù)。
= 度;
= 度。
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 是等邊
是等邊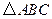 內(nèi)一點,
內(nèi)一點,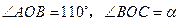 .將
.將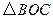 繞點
繞點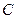 按順時針方向旋轉
按順時針方向旋轉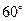 得
得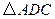 ,連接
,連接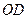
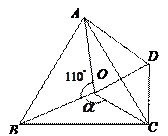
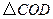 是等邊三角形;
是等邊三角形;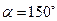 時,試判斷
時,試判斷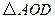 的形狀,并說明理由
的形狀,并說明理由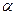 為多少度時,
為多少度時,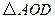 是等腰三角形?
是等腰三角形?查看答案和解析>>
科目:初中數(shù)學 來源:2013年北京市通州區(qū)中考二模數(shù)學試卷(解析版) 題型:解答題
如圖,點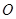 是等邊
是等邊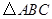 內(nèi)一點,
內(nèi)一點,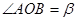 ,
, 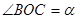 .將
.將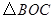 繞點
繞點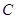 按順時針方向旋轉
按順時針方向旋轉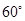 得
得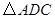 ,連接
,連接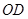 .
.
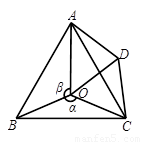
(1)當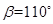 ,
,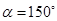 時,試判斷
時,試判斷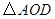 的形狀,并說明理由.
的形狀,并說明理由.
(2)請寫出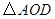 是等邊三角形時
是等邊三角形時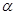 、
、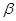 的度數(shù).
的度數(shù).
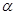 = 度;
= 度;
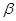 = 度.
= 度.
(3)探究:若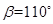 ,則
,則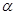 為多少度時,
為多少度時,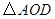 是等腰三角形?
是等腰三角形?
(只要寫出探究結果)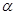 = ;
= ;
查看答案和解析>>
科目:初中數(shù)學 來源:2012屆河南大學附中九年級上學期期中考試數(shù)學試卷 題型:解答題
如圖,點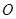 是等邊
是等邊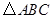 內(nèi)一點,
內(nèi)一點,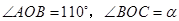 .將
.將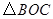 繞點
繞點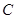 按順時針方向旋轉
按順時針方向旋轉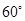 得
得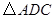 ,連接
,連接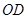

1.求證: 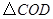 是等邊三角形;
是等邊三角形;
2.當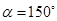 時,試判斷
時,試判斷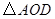 的形狀,并說明理由
的形狀,并說明理由
3.探究:當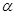 為多少度時,
為多少度時,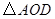 是等腰三角形?
是等腰三角形?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com