
【題目】如下數(shù)表是由從1 開始的連續(xù)自然數(shù)組成,觀察規(guī)律并完成各題的解答.

(1)表中第8行的最后一個數(shù)是_____,它是自然數(shù)_____的平方,第8行共有 _____個數(shù);
(2)用含n的代數(shù)式表示:第n行的第一個數(shù)是_____,最后一個數(shù)是_____,第n行共有_____個數(shù);
(3)求第n行各數(shù)之和.
【答案】(1)64,8,15;
(2)(n-1)2+1,n2,2n-1,
(3)![]()
【解析】
(1)先從給的數(shù)中得出每行最后一個數(shù)是該行的平方,即可求出第8行的最后一個數(shù),再根據(jù)每行的個數(shù)為1,3,5,…的奇數(shù)列,即可求出第8行共有的個數(shù);(2)根據(jù)第n行最后一個數(shù)為n2,得出第一個數(shù)為n2-2n+2,根據(jù)每行的個數(shù)為1,3,5,…,即可得出答案;(3)通過(2)得出的第n行的第一個數(shù)與最后一個數(shù)及第n行共有的個數(shù),列出算式,進行計算即可.
(1)先從給的數(shù)中得出每行最后一個數(shù)是該行的平方,則第8行的最后一個數(shù)是82=64,
每行數(shù)的個數(shù)為1,3,5,…的奇數(shù)列,
∴第8行共有8×2-1=15個;
故答案為64,8,15;
(2)由(1)知第n行最后一個數(shù)是n2,
則得出第一個數(shù)為n2-2n+2
第n行共有2n-1個數(shù)
故答案為n2,2n-1;
(3)∵第n行第一個數(shù)為n2-2n+2,最后一個數(shù)為n2,共有2n-1個數(shù)
∴第n各數(shù)之和為![]()


科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知在平面直角坐標系中,如圖,點![]() ,點
,點![]() ,連接
,連接![]() ,過點B作直線
,過點B作直線![]() 交
交![]() 于A點,設(shè)直線
于A點,設(shè)直線![]() 的解析式為
的解析式為![]()
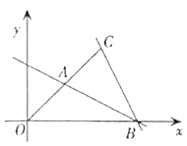
(1)求直線![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)若直線![]() 平分
平分![]() 的面積時,求A到x軸的距離;
的面積時,求A到x軸的距離;
(3)作點C關(guān)于y軸的對稱點D,若直線![]() 與線段
與線段![]() 有交點,求k的取值范圍.
有交點,求k的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線![]() 與坐標軸交于點
與坐標軸交于點![]() 、
、![]() 兩點,直線
兩點,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,交
,交![]() 軸于點
軸于點![]() ,且
,且![]() 的面積為
的面積為![]() .
.

(1)求![]() 的值和點
的值和點![]() 的坐標;
的坐標;
(2)求直線![]() 的解析式;
的解析式;
(3)若點![]() 是線段
是線段![]() 上一動點,過點
上一動點,過點![]() 作
作![]() 軸交直線
軸交直線![]() 于點
于點![]() ,
,![]() 軸,
軸,![]() 軸,垂足分別為點
軸,垂足分別為點![]() 、
、![]() ,是否存在點
,是否存在點![]() ,使得四邊形
,使得四邊形![]() 為正方形,若存在,請求出點
為正方形,若存在,請求出點![]() 坐標,若不存在,請說明理由.
坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,點O是邊AC上一個動點,過O作直線MN∥BC,設(shè)MN交∠BCA的平分線于點E,交∠BCA的外角平分線于點F.

(1)探究:線段OE與OF的數(shù)量關(guān)系并加以證明;
(2)當點O在邊AC上運動時,四邊形BCFE會是菱形嗎?若是,請證明;若不是,則說明理由;
(3)當點O運動到何處,且△ABC滿足什么條件時,四邊形AECF是正方形?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】用大小相等的小正方形按一定規(guī)律拼成下列圖形.
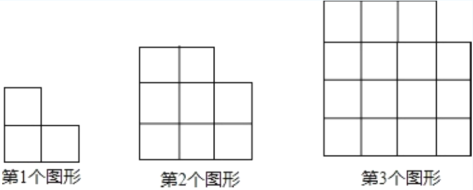
⑴第4個圖形中小正方形的個數(shù)是______;
⑵第![]() 個圖形中小正方形的個數(shù)是多少?
個圖形中小正方形的個數(shù)是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將下列各數(shù)填到相應(yīng)的集合里:
-![]() ,+5,-9,π,
,+5,-9,π,![]() ,19, 1.2, 0,-5.26,0.8256…,5.3
,19, 1.2, 0,-5.26,0.8256…,5.3
正數(shù)集合﹛ …﹜
負數(shù)集合﹛ …﹜
整數(shù)集合﹛ …﹜
分數(shù)集合﹛ …﹜
有理數(shù)集合﹛ …﹜
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知∠AED=∠C,∠1+∠2=180°.請說明∠BEC=∠FGC
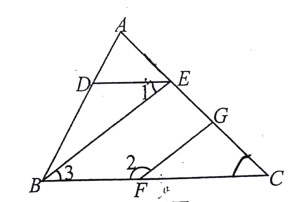
解:因為∠AED=∠C(已知),
所以________∥_______(_________________________________ )
得∠1=∠3( _______________________________ )
又∠1+∠2=180°(已知),
得∠3+∠2=180°(___________________________)
所以_______∥_______
所以∠BEC=∠FGC(___________________________)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=4,BC=3.點E從點A出發(fā),以每秒4個單位長度的速度沿折線AC-CB運動,到點B停止.當點E不與△ABC的頂點重合時,過點E作其所在直角邊的垂線交AB于點F,將△AEF繞點F沿逆時針方向旋轉(zhuǎn)得到△NMF,使點A的對應(yīng)點N落在射線FE上.設(shè)點E的運動時間為t(秒).
(1)用含t的代數(shù)式表示線段CE的長.
(2)求點M落到邊BC上時t的值.
(3)當點E在邊AC上運動時,設(shè)△NMF與△ABC重疊部分圖形為四邊形時,四邊形的面積為S(平方單位),求S與t之間的函數(shù)關(guān)系式.
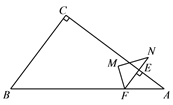
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
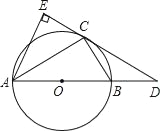
【題目】如圖,已知⊙O是△ABC的外接圓,AB是⊙O的直徑,D是AB延長線上一點,AE⊥DC交DC的延長線于點E,且AC平分∠EAB.
(1)求證:DE是⊙O的切線;
(2)若AB=6,AE=![]() ,求BD和BC的長.
,求BD和BC的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com