
【題目】若直線![]() 與函數(shù)
與函數(shù)![]() 的圖象有唯一公共點,則
的圖象有唯一公共點,則![]() 的值為__ ;有四個公共點時,
的值為__ ;有四個公共點時,![]() 的取值范圍是_
的取值范圍是_
【答案】-3 ![]()
【解析】
根據(jù)函數(shù)y=|x2-2x-3|與直線y=x+m的圖象之間的位置關(guān)系即可求出答案.
解:作出y=|x2-2x-3|的圖象,如圖所示,
∴y=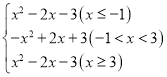 ,
,
當(dāng)直線y=x+m與函數(shù)y=|x2-2x-3|的圖象只有1個交點時,
直線經(jīng)過點(3,0),將(3,0)代入直線y=x+m,
得m=-3,
聯(lián)立![]() ,
,
消去y后可得:x2-x+m-3=0,
令△=0,
可得:1-4(m-3)=0,
m=![]() ,
,
即m=![]() 時,直線y=x+m與函數(shù)y=|x2-2x-3|的圖象只有3個交點,
時,直線y=x+m與函數(shù)y=|x2-2x-3|的圖象只有3個交點,
當(dāng)直線過點(-1,0)時,
此時m=1,直線y=x+m與函數(shù)y=|x2-2x-3|的圖象只有3個交點,
∴直線y=x+m與函數(shù)y=|x2-2x-3|的圖象有四個公共點時,m的范圍為:![]() ,
,
故答案為:-3,![]() .
.
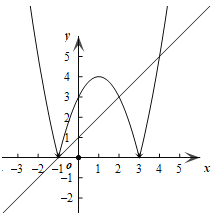


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側(cè)),與
的左側(cè)),與![]() 軸交于點
軸交于點![]() .
.
(1)如圖1,若點![]() 是直線
是直線![]() 上方拋物線上的一個動點,過點
上方拋物線上的一個動點,過點![]() 作
作![]() 軸交直線
軸交直線![]() 于點
于點![]() ,作
,作![]() 于點
于點![]() ,點
,點![]() 為直線
為直線![]() 上一動點,點
上一動點,點![]() 為
為![]() 軸上一動點,連接
軸上一動點,連接![]() ,
,![]() .當(dāng)
.當(dāng)![]() 最長時,求
最長時,求![]() 的最小值;
的最小值;
(2)如圖2,將![]() 繞點
繞點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得
得![]() ,將
,將![]() 沿直線
沿直線![]() 平移得到
平移得到![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,將
,將![]() 沿邊
沿邊![]() 翻折得
翻折得![]() ,連接
,連接![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 是等腰三角形時,求此時點
是等腰三角形時,求此時點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
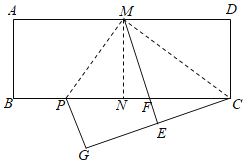
【題目】如圖,在矩形ABCD中,AD=2![]() AB.將矩形ABCD對折,得到折痕MN,沿著CM折疊,點D的對應(yīng)點為E,ME與BC的交點為F;再沿著MP折疊,使得AM與EM重合,折痕為MP,此時點B的對應(yīng)點為G.下列結(jié)論:①△CMP是直角三角形;②AB=
AB.將矩形ABCD對折,得到折痕MN,沿著CM折疊,點D的對應(yīng)點為E,ME與BC的交點為F;再沿著MP折疊,使得AM與EM重合,折痕為MP,此時點B的對應(yīng)點為G.下列結(jié)論:①△CMP是直角三角形;②AB=![]() BP;③PN=PG;④PM=PF;⑤若連接PE,則△PEG∽△CMD.其中正確的個數(shù)為( )
BP;③PN=PG;④PM=PF;⑤若連接PE,則△PEG∽△CMD.其中正確的個數(shù)為( )
A.5個B.4個C.3個D.2個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】解方程:
(1)3(2x+1)2=108
(2)3x(x-1)=2-2x
(3)x2-6x+9=(5-2x)2
(4)x(2x-4)=5-8x
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() ,下列說法正確的是( )
,下列說法正確的是( )
A.該函數(shù)的圖象的開口向下B.該函數(shù)圖象的頂點坐標(biāo)是![]()
C.當(dāng)![]() 時,
時,![]() 隨
隨![]() 的增大而增大D.該函數(shù)的圖象與
的增大而增大D.該函數(shù)的圖象與![]() 軸有兩個不同的交點
軸有兩個不同的交點
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】矩形ABCD中,AB=6,BC=8.點P在矩形ABCD的內(nèi)部,點E在邊BC上,滿足△PBE∽△DBC,若△APD是等腰三角形,則PE的長為數(shù)___________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】廊橋是我國古老的文化遺產(chǎn).如圖,是某座拋物線型的廊橋示意圖,已知拋物線的函數(shù)表達式為![]() ,為保護廊橋的安全,在該拋物線上距水面
,為保護廊橋的安全,在該拋物線上距水面![]() 高為8米的點
高為8米的點![]() 、
、![]() 處要安裝兩盞警示燈,則這兩盞燈的水平距離
處要安裝兩盞警示燈,則這兩盞燈的水平距離![]() 是____米.
是____米.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】嘉善縣將開展以“珍愛生命,鐵拳護航”為主題的交通知識競賽,某校對參加選拔賽的若干名同學(xué)的成績按A,B,C,D四個等級進行統(tǒng)計,繪制成如下不完整的頻數(shù)統(tǒng)計表和扇形統(tǒng)計圖
成績等級 | 頻數(shù)(人數(shù)) | 頻率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合計 | 1 |
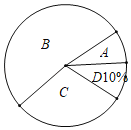
(1)求m= ,n= ;
(2)在扇形統(tǒng)計圖中,求“C等級”所對應(yīng)圓心角的度數(shù);
(3)“A等級”的4名同學(xué)中有3名男生和1名女生,現(xiàn)從中隨機挑選2名同學(xué)代表學(xué)校參加全縣比賽,請用樹狀圖法或列表法求出恰好選中“一男一女”的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示,過點(0,1)和(﹣1,0),給出以下結(jié)論:①ab<0;②4a+c<1+b2;③0<c+b+a<2;④0<b<2;⑤當(dāng)x>﹣1時,y>0;⑥8a+7b+2c﹣9<0其中正確結(jié)論的個數(shù)是( )
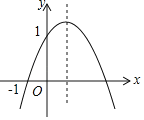
A.6B.5C.4D.3
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com