【題目】已知⊙O經過四邊形ABCD的B、D兩點，并與四條邊分別交于點E、F、G、H，且
．
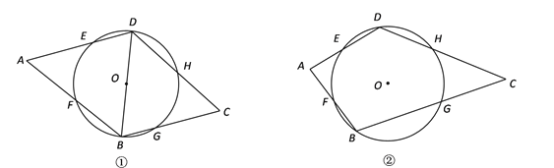
（1）如圖①，連接BD，若BD是⊙O的直徑，求證：∠A＝∠C；
（2）如圖②，若
的度數為θ，∠A＝α，∠C＝β，請直接寫出θ、α和β之間的數量關系．
【答案】（1）證明見解析；（2）α+β+θ =180°
【解析】
（1）根據圓周角定理及同弧所對的圓周角相等，得到∠EDF＝∠HDG，然后利用外角的性質等量代換求證；
（2）利用外角性質及圓內接四邊形對角互補求解.
（1） 連接DF、DG
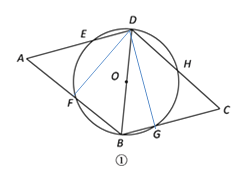
∵BD是⊙O的直徑
∴∠DFB＝∠DGB =90°，
∵
∴∠EDF＝∠HDG，
∵∠DFB＝∠EDF+∠A
∠DGB＝∠HDG+∠C，
∴∠A＝∠C
（2）
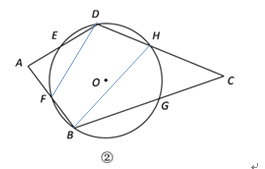
連接DF,BH
∵
∴∠ADF=∠HBG=
θ
又∵∠DFB=∠A+∠ADF,∠DHB=∠C+∠HBG
∴∠DFB+∠DHB=∠A+∠ADF+∠C+∠HBG
根據圓內接四邊形對角互補，可得
∴α+β+θ =180°
科目：初中數學 來源： 題型：
【題目】已知：如圖，在同心圓中，大圓的弦AB交小圓于C、D兩點．
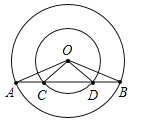
（1）求證：∠AOC=∠BOD；
（2）試確定AC與BD兩線段之間的大小關系，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AB＝AC＝2，∠BAC＝45°，△AEF是由△ABC繞點A按逆時針方向旋轉得到的，連接BE、CF相交于點D．
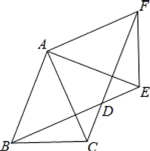
（1）求證：BE＝CF；
（2）當四邊形ABDF為菱形時，求CD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
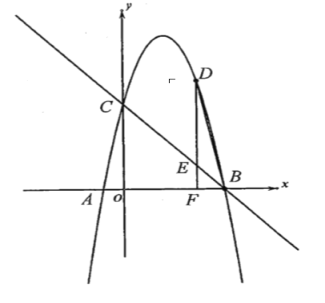
【題目】如圖，已知拋物線
與
軸交于
，
兩點，（點在點的左邊），與
軸交于點
.
（1）求點，，的坐標；
（2）點
是第一象限內拋物線上的一個動點（與點，不重合），過點作
軸于點
，交直線
于點
，連接
，直線能否把
分成面積之比為2：3的兩部分？若能，請求出點的坐標；若不能，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠A＝90°，∠B＝36°，點D為斜邊BC的中點，將線段DC繞著點D逆時針旋轉任意角度得到線段DE（點E不與A、B、C重合），連接EA，EC，則∠AEC＝___________°.
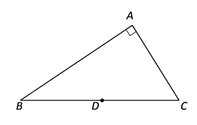
查看答案和解析>>
科目：初中數學 來源： 題型：
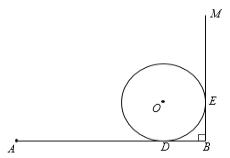
【題目】如圖，∠ABM＝90°，⊙O分別切AB、BM于點D、E．AC切⊙O于點F，交BM于點C（C與B不重合）．
（1）用直尺和圓規作出AC（保留作圖痕跡，不寫作法）；
（2）若⊙O半徑為1，AD＝4，求AC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AC是⊙O的直徑，弦BD⊥AO于E，連接BC，過點O作OF⊥BC于F，若BD＝16cm，AE＝4cm．
（1）求⊙O的半徑；
（2）求OF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點C是半圓O上的一點，AB是⊙O的直徑，D是
的中點，作DE⊥AB于點E，連接AC交DE于點F，求證：AF=DF.
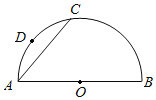
下面是小明的做法，請幫他補充完整（包括補全圖形）
解：補全半圓O為完整的⊙O，連接AD，延長DE交⊙O于點H（補全圖形）
∵D是的中點，
∴
.
∵DE⊥AB，AB是⊙O的直徑，
∴
（ ）（填推理依據）
∴
∴∠ADF=∠FAD（ ）（填推理依據）
∴AF=DF（ ）（填推理依據）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
