
分析 根據k=$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$即可得出k=1或-2,由n2+16+$\sqrt{m+6}$=8n利用偶次方及被開方數非零即可得出m、n的值,進而可得出n-m的值,再根據一次函數圖象與系數的關系即可得出一次函數經過的象限,此題得解.
解答 解:∵k=$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$,
∴a=b=c,k=1或a+b=-c,k=-2.
∵n2+16+$\sqrt{m+6}$=8n,
∴(n-4)2+$\sqrt{m+6}$=0,
∴m=-6,n=4,
∴n-m=10>0,
∴一次函數y=kx+n-m的圖象經過第一、二、三象限或第一、二、四象限.
故答案為:1或-2;一、二.
點評 本題考查了一次函數圖象與系數的關系以及偶次方及被開方數非零,通過解方程組以及偶次方和被開方數非零求出k和n-m的值是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
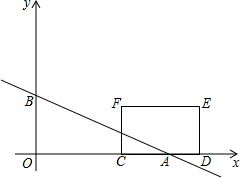 如圖,在平面直角坐標系中,直線y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分別交x軸、y軸于A、B兩點,點C(3,0),D(6,0),以CD為一邊在x軸上方作矩形CDEF,CF=$\sqrt{3}$,設矩形CDEF與△ABO重疊部分的面積為S.
如圖,在平面直角坐標系中,直線y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分別交x軸、y軸于A、B兩點,點C(3,0),D(6,0),以CD為一邊在x軸上方作矩形CDEF,CF=$\sqrt{3}$,設矩形CDEF與△ABO重疊部分的面積為S.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
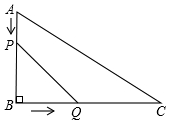 如圖,在△ABC中,∠B=90°,AB=12mm,BC=24mm,動點P以2mm/s的速度從A向B移動,(不與B重合),動點Q以4mm/s的速度從B向C移動,(不與C重合),若P、Q同時出發,試問:
如圖,在△ABC中,∠B=90°,AB=12mm,BC=24mm,動點P以2mm/s的速度從A向B移動,(不與B重合),動點Q以4mm/s的速度從B向C移動,(不與C重合),若P、Q同時出發,試問:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
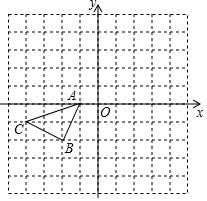 在直角坐標系中,△ABC的三個頂點的位置如圖所示:
在直角坐標系中,△ABC的三個頂點的位置如圖所示:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com