
【題目】武漢二中廣雅中學為了進一步改進本校九年級數學教學,提高學生學習數學的興趣.校教務處在九年級所有班級中,每班隨機抽取了6名學生,并對他們的數學學習情況進行了問卷調查:我們從所調查的題目中,特別把學生對數學學習喜歡程度的回答(喜歡程度分為:“![]() 非常喜歡”、“
非常喜歡”、“ ![]() 比較喜歡”、“
比較喜歡”、“ ![]() 不太喜歡”、“
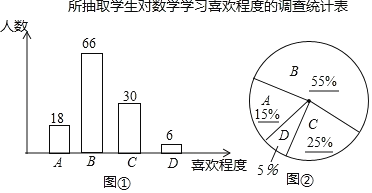
不太喜歡”、“ ![]() 很不喜歡”,針對這個題目,問卷時要求每位被調查的學生必須從中選一項且只能選一項)結果進行了統計.現將統計結果繪制成如下兩幅不完整的統計圖.
很不喜歡”,針對這個題目,問卷時要求每位被調查的學生必須從中選一項且只能選一項)結果進行了統計.現將統計結果繪制成如下兩幅不完整的統計圖.

請你根據以上提供的信息,解答下列問題:
(1)補全上面的條形統計圖和扇形統計圖;
(2)所抽取學生對數學學習喜歡程度的眾數是 ,圖②中![]() 所在扇形對應的圓心角是 ;
所在扇形對應的圓心角是 ;
(3)若該校九年級共有960名學生,請你估算該年級學生中對數學學習“不太喜歡”的有多少人?
【答案】(1)答案見解析;(2)B,54°;(3)240人.
【解析】
(1)根據D程度的人數和所占抽查總人數的百分率即可求出抽查總人數,然后利用總人數減去A、B、D程度的人數即可求出C程度的人數,然后分別計算出各程度人數占抽查總人數的百分率,從而補全統計圖即可;
(2)根據眾數的定義即可得出結論,然后利用360°乘A程度的人數所占抽查總人數的百分率即可得出結論;
(3)利用960乘C程度的人數所占抽查總人數的百分率即可.
解:(1)被調查的學生總人數為![]() 人,
人,
C程度的人數為![]() 人,
人,
則![]() 的百分比為
的百分比為![]() 、
、![]() 的百分比為
的百分比為![]() 、
、![]() 的百分比為
的百分比為![]() ,
,
補全圖形如下:
(2)所抽取學生對數學學習喜歡程度的眾數是![]() 、圖②中
、圖②中![]() 所在扇形對應的圓心角是
所在扇形對應的圓心角是![]() .
.
故答案為:![]() ;
;![]() ;
;
(3)該年級學生中對數學學習“不太喜歡”的有![]() 人
人
答:該年級學生中對數學學習“不太喜歡”的有240人.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】隨著生活水平的提高,人們對飲水品質的需求越來越高,某公司根據市場需求代理A,B兩種型號的凈水器,每臺A型凈水器比每臺B型凈水器進價多200元,用5萬元購進A型凈水器與用4.5萬元購進B型凈水器的數量相等
(1)求每臺A型、B型凈水器的進價各是多少元?
(2)該公司計劃購進A,B兩種型號的凈水器共50臺進行試銷,其中A型凈水器為x臺,購買資金不超過9.8萬元,試銷時A型凈水器每臺售價2500元,B型凈水器每臺售價2180元,公司決定從銷售A型凈水器的利潤中按每臺捐獻a元作為公司幫扶貧困村飲水改造資金.若公司售完50臺凈水器并捐獻扶貧資金后獲得的最大利潤不低于20200元但不超過23000元,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
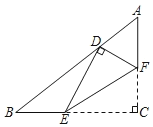
【題目】如圖,在Rt△ABC中,∠C=90°,AB=5,BC=4,點E,F分別在邊BC,AC上,沿EF所在的直線折疊∠C,使點C的對應點D恰好落在邊AB上,若△EFC和△ABC相似,則BD的長為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上.

(1)畫出△ABC關于原點對稱的△A1B1C1;
(2)畫出△ABC向上平移5個單位后的△A2B2C2,并求出平移過程中△ABC掃過的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
在數學活動課上,老師出示了這樣一個問題:如圖1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 邊上的任意一點.將
邊上的任意一點.將![]() 沿過點
沿過點![]() 的直線折疊,使點
的直線折疊,使點![]() 落在斜邊
落在斜邊![]() 上的點
上的點![]() 處.問是否存在
處.問是否存在![]() 是直角三角形?若不存在,請說明理由;若存在,求出此時
是直角三角形?若不存在,請說明理由;若存在,求出此時![]() 的長度.
的長度.

探究展示:勤奮小組很快找到了點![]() 、
、![]() 的位置.
的位置.
如圖2,作![]() 的角平分線交
的角平分線交![]() 于點
于點![]() ,此時
,此時![]() 沿
沿![]() 所在的直線折疊,點
所在的直線折疊,點![]() 恰好在
恰好在![]() 上,且
上,且![]() ,所以
,所以![]() 是直角三角形.
是直角三角形.
問題解決:
(1)按勤奮小組的這種折疊方式,![]() 的長度為 .
的長度為 .
(2/span>)創新小組看完勤奮小組的折疊方法后,發現還有另一種折疊方法,請在圖3中畫出來.
(3)在(2)的條件下,求出![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() ,
,![]() 兩點
兩點![]() 在
在![]() 左側),與
左側),與![]() 軸交于點
軸交于點![]() ,頂點為
,頂點為![]() .
.
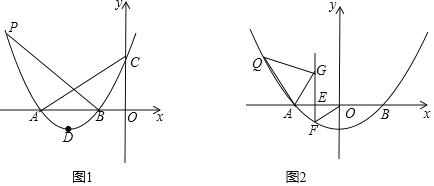
(1)當![]() 時,求四邊形
時,求四邊形![]() 的面積
的面積![]() ;
;
(2)在(1)的條件下,在第二象限拋物線對稱軸左側上存在一點![]() ,使
,使![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)如圖2,將(1)中拋物線沿直線![]() 向斜上方向平移
向斜上方向平移![]() 個單位時,點
個單位時,點![]() 為線段
為線段![]() 上一動點,
上一動點,![]() 軸交新拋物線于點
軸交新拋物線于點![]() ,延長
,延長![]() 至
至![]() ,且
,且![]() ,若
,若![]() 的外角平分線交點
的外角平分線交點![]() 在新拋物線上,求
在新拋物線上,求![]() 點坐標.
點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=a(x-1)2+k與x軸兩個交點間的距離為2,將拋物線y=a(x-1)2+k向上平移n個單位,平移后的拋物線經過點(m,n),則m的值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數與x軸,y軸的交點分別是A(﹣4,0),B(0,2).與反比例函數的圖象交于點Q,反比例函數圖象上有一點P滿足:①PA⊥x軸;②PO=![]() (O為坐標原點),則四邊形PAQO的面積為( )
(O為坐標原點),則四邊形PAQO的面積為( )

A.7B.10C.4+2![]() D.4﹣2
D.4﹣2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以40m/s的速度將小球沿與地面成30°角的方向擊出時,小球的飛行路線將是一條拋物線.如果不考慮空氣阻力,小球的飛行高度h(單位:m)與飛行時間t(單位:s)之間具有函數關系h=20t﹣5t2.下列敘述正確的是( )

A. 小球的飛行高度不能達到15m
B. 小球的飛行高度可以達到25m
C. 小球從飛出到落地要用時4s
D. 小球飛出1s時的飛行高度為10m
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com