【題目】P是△ABC的內心，BC=4，∠BAC=90°,則△PBC的外接圓半徑為________．
【答案】
【解析】
作如下所示圖，先求出∠BPC的度數，再利用圓內接四邊形對角互補求出∠BQC的度數，再由圓周角定理求出∠BOC度數，進而得到△BOC是等腰直角三角形，進而求解.
解：作如下所示圖，P為△ABC的內心，圓O為△PBC的外接圓，∠BAC=90°
由內心的定義可知，BP、CP、AP分別是∠ABC、∠ACB、∠BAC的角平分線，
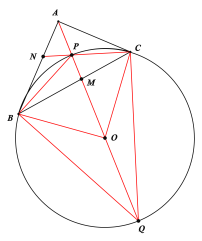
∴∠BPC=180°-(∠PBC+∠PCB)=180°-(
∠ABC+∠ACB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠BAC)=180°-×90°=135°.
由圓內接四邊形對角互補知：∠BQC+∠BPC=180°
∴∠BQC=180°-∠BPC=45°
由同弧所對的圓周角等于圓心角的一半知：
∠BOC=2∠BQC=90°
且BO=CO，
∴△BOC為等腰直角三角形，
由BC=4可知，BO=
.
故答案為：.
特高級教師點撥系列答案科目：初中數學 來源： 題型：
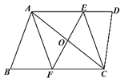
【題目】如圖，在四邊形ABCD中，AD∥BC，點O是對角線AC的中點，過點O作AC的垂線，分別交AD、BC于點E、F，連接AF、CE.試判斷四邊形AECF的形狀，并證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
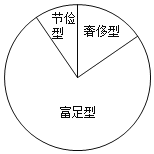
【題目】某校為了解學生零用錢支出情況，從七、八、九年級800名學生中隨機抽取部分學生，對他們今年5月份的零用錢支出情況進行調查統計，并繪制成如下統計圖表：
組別 | 零用錢支出x（單位：元） | 頻數（人數） | 頻率 | |
節儉型 | 一 | x＜20 | m | 0.05 |
二 | 20≤x＜30 | 4 | a | |
富足型 | 三 | 30≤x＜40 | n | 0.45 |
四 | 40≤x＜50 | 12 | b | |
奢侈型 | 五 | x≥50 | 4 | c |
合計 | 1 | |||
（1）表中a+b+c＝ ；m＝ ；本次調查共隨機抽取了 名同學；
（2）在扇形統計圖中，“富足型”對應的扇形的圓心角的度數是 ；
（3）估計今年5月份全校零花錢支出在30≤x＜40范圍內的學生人數；
（4）在抽樣的“奢侈型”學生中，有2名女生和2名男生．學校團委計劃從中隨機抽取2名同學參加“綠苗理財計劃”活動，請運用樹狀圖或者列表說明恰好抽到一男一女的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市在九年級“線上教學”結束后，為了了解學生的視力情況，抽查了部分學生進行視力檢查．根據檢查結果，制作下面不完整的統計圖表．
（1）求組別C的頻數m的值．
（2）求組別A的圓心角度數．
（3）如果勢視力值4．8及以上屬于“視力良好”，請估計該市25000名九年級學生達到“視力良好”的人數，根據上述圖表信息，你對視力保護有什么建議？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC=5，BC=4
,D為邊AB上一動點(B點除外)，以CD為一邊作正方形CDEF，連接BE，則△BDE面積的最大值為______.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】平面直角坐標系中，拋物線C1：y1=x2-2mx+2m2-1，拋物線C2：y2=x2-2nx+2n2-1，
（1）若m=2，過點A(0,7)作直線l垂直于y軸交拋物線C1于點B、C兩點．
①求BC的長；
②若拋物線C2與直線l交于點E、F兩點，若EF長大于BC的長，直接寫出n的范圍；
（2）若m+n=k(k是常數)，
①若
，試說明拋物線C1與拋物線C2的交點始終在定直線上；
②求y1+y2的最小值(用含k的代數式表示) ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）問題發現
如圖①，
是等腰直角三角形，四邊形
是正方形，點
與點
重合，則線段
與
之間的數量關系和位置關系分別是 ．
（2）深入探究
如圖②，是等腰直角三角形，四邊形是正方形，點
在直線
上，對角線
所在的直線交直線于點
，則線段
之間有什么數量關系？請僅就圖②給出證明．
（3）拓展思維
如圖②，若點在直線上，且線段
，當
時，直接寫出此時正方形的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，
，
于點D，
于點E，交AD于點F，點M是BC的中點，連接FM并延長交AB的垂線BH于點H．下列說法中錯誤的是（ ）
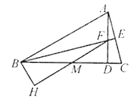
A.若
，則
B.若
，則
C.若
（點M與點D重合），則
D.若
（點B與點D重合），則
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某水產養殖戶開發一個三角形狀的養殖區域，A、B、C三點的位置如圖所示．已知∠CAB=105°，∠B=45°，AB=100
米．（參考數據：≈1．41，
≈1．73，sin20°≈0．34，cos20°≈0．94，tan20°≈0．36，結果保留整數）
（1）求養殖區域△ABC的面積；
（2）養殖戶計劃在邊BC上選一點D，修建垂釣棧道AD，測得∠CAD=40°，求垂釣棧道AD的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com