
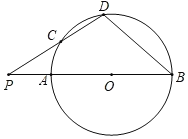
【題目】如圖,AB為![]() 的直徑,P為BA延長線上的一點,D在
的直徑,P為BA延長線上的一點,D在![]() 上(不與點A,點B重合),連結PD交
上(不與點A,點B重合),連結PD交![]() 于點C,且PC=OB.設
于點C,且PC=OB.設![]() ,下列說法正確的是( )
,下列說法正確的是( )
A. 若![]() ,則
,則![]()
B. 若![]() ,則
,則![]()
C. 若![]() ,則
,則![]()
D. 若![]() ,則
,則![]()
【答案】C
【解析】
連接OC,OD.首先證明3α+2β=180°,再一一判斷即可.
如圖,連接OC,OD.

∵OD=OB,∴∠B=∠ODB=β,∴∠POD=∠B+∠ODB=2β.
∵CP=CO=OD,∴∠P=∠COP=α,∠OCD=∠ODC.
∵∠OCD=∠P+∠COP,∴∠ODC=2α.
∵∠P+∠POD+∠ODP=180°,∴3α+2β=180°①.
不妨設選項A正確,則α=30°,β=30°,顯然不滿足①,故假設錯誤.
不妨設B正確,則α=30°,β=60°,顯然不滿足①,故假設錯誤.
不妨設C正確,則α=10°,β=75°,滿足條件①,故選項C正確.
不妨設B正確,則α=15°,β=45°,顯然不滿足①,故假設錯誤.
故選C.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:初中數學 來源: 題型:
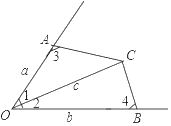
【題目】如圖,在四邊形AOBC中,若∠1=∠2,∠3+∠4=180°,則下列結論正確的有( )
(1)A、O、B、C四點共圓
(2)AC=BC
(3)cos∠1=![]()
(4)S四邊形AOBC=![]()
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
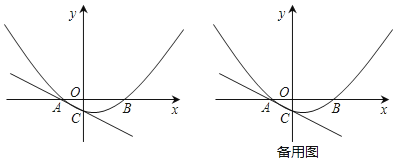
【題目】如圖,已知A(﹣2,0),B(4,0),拋物線y=ax2+bx﹣1過A、B兩點,并與過A點的直線y=﹣![]() x﹣1交于點C.
x﹣1交于點C.
(1)求拋物線解析式及對稱軸;
(2)在拋物線的對稱軸上是否存在一點P,使四邊形ACPO的周長最小?若存在,求出點P的坐標,若不存在,請說明理由;
(3)點M為y軸右側拋物線上一點,過點M作直線AC的垂線,垂足為N.問:是否存在這樣的點N,使以點M、N、C為頂點的三角形與△AOC相似,若存在,求出點N的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
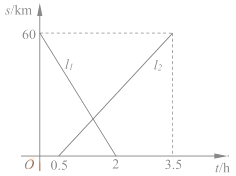
【題目】A、B兩地相距60km,甲、乙兩人從兩地出發相向而行,甲先出發.圖中![]() 表示兩人離A地的距離S(km)與時間t(h)的關系,結合圖像回答下列問題:
表示兩人離A地的距離S(km)與時間t(h)的關系,結合圖像回答下列問題:
(1)表示乙離開A地的距離與時間關系的圖像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出發后多少時間兩人恰好相距5km?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用兩個全等的等邊三角形△ABC和△ACD拼成菱形ABCD.把一個含60°角的三角尺與這個菱形疊合,使三角尺的60°角的頂點與點A重合,兩邊分別與AB,AC重合.將三角尺繞點A按逆時針方向旋轉.
(1)當三角尺的兩邊分別與菱形的兩邊BC,CD相交于點E,F時,(如圖1),通過觀察或測量BE,CF的長度,你能得出什么結論并證明你的結論;
(2)當三角尺的兩邊分別與菱形的兩邊BC,CD的延長線相交于點E,F時(如圖2),你在(1)中得到的結論還成立嗎?簡要說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,兩條射線BA//CD,PB和PC分別平分∠ABC和∠DCB,AD過點P,分別交AB,CD與點A,D.
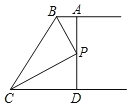
(1)求∠BPC的度數;
(2)若![]() ,求AB+CD的值;
,求AB+CD的值;
(3)若![]() 為a,
為a,![]() 為b,
為b,![]() 為c,求證:a+b=c.
為c,求證:a+b=c.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在平面直角坐標系中反比例函數y=![]() 的圖象經過點P(4,3)和點B(m,n)(其中0<m<4),作BA⊥x軸于點A,連接PA、OB,過P、B兩點作直線PB,且S△AOB=S△PAB
的圖象經過點P(4,3)和點B(m,n)(其中0<m<4),作BA⊥x軸于點A,連接PA、OB,過P、B兩點作直線PB,且S△AOB=S△PAB
(1)求反比例函數的解析式;
(2)求點B的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC放在以O為原點的平面直角坐標系中,A(3,0),C(0,2),點E是AB的中點,點F在BC邊上,且CF=1,若M為x軸上的動點,N為y軸上的動點,則四邊形MNFE的周長最小值是_____.
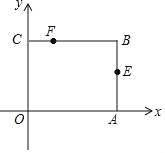
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】婷婷在發現一個門環的示意圖如圖所示.圖中以正六邊形ABCDEF的對角線AC的中點O為圓心,OB為半徑作⊙O,AQ切⊙O于點P,并交DE于點Q,若AQ=12![]() cm,則該圓的半徑為_____cm.
cm,則該圓的半徑為_____cm.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com