
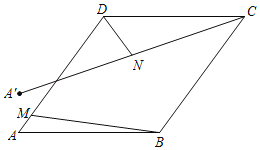
【題目】如圖,菱形ABCD的邊長為10,sinA=![]() ,點M為邊AD上的一個動點且不與點A和點D重合,點A關于直線BM的對稱點為點A',點N為線段CA'的中點,連接DN,則線段DN長度的最小值是_____.
,點M為邊AD上的一個動點且不與點A和點D重合,點A關于直線BM的對稱點為點A',點N為線段CA'的中點,連接DN,則線段DN長度的最小值是_____.
【答案】![]() ﹣5.
﹣5.
【解析】
通過構造三邊關系來求DN的最小值,根據A,A'關于直線BM對稱,BA′=10,取BC的中點K,NK是![]() 的中位線,NK=5,作DH⊥BC,根據sinA=
的中位線,NK=5,作DH⊥BC,根據sinA=![]() 可求出DH=8,CH=6,在Rt△DHK中,由勾股定理求得DK的值,看△DNK根據三角形的三邊關系即可求出答案.
可求出DH=8,CH=6,在Rt△DHK中,由勾股定理求得DK的值,看△DNK根據三角形的三邊關系即可求出答案.
解:如圖,連接BA′,取BC的中點K,連接NK,作DH⊥BC于H.

∵四邊形ABCD是菱形,
∴AB=BC=CD=AD=10,∠A=∠DCB,
∵A,A′關于BM對稱,
∴BA′=BA=10,
∵CN=NA′,CK=BK,
∴NK=![]() BA′=5,
BA′=5,
∵sin∠A=sin∠DCH=![]() =
=![]() ,
,
∴DH=8,
∴CH=![]() =
=![]() =6,
=6,
∴CK=KB=5,
∴HK=CH=CK=1,
∴DK=![]() =
=![]() =
=![]() ,
,
∵DN≥DK﹣NK,
∴DN≥![]() ﹣5,
﹣5,
∴DN的最小值為![]() ﹣5,
﹣5,
故答案為:![]() ﹣5.
﹣5.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】(1)問題發(fā)現(xiàn)
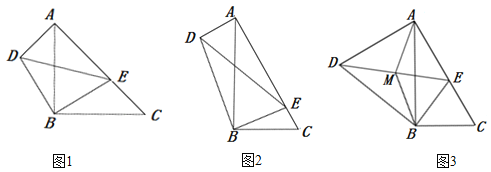
如圖1,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=45°,點E是線段AC上一動點,連接DE.
填空:①則![]() 的值為______;②∠EAD的度數(shù)為_______.
的值為______;②∠EAD的度數(shù)為_______.
(2)類比探究
如圖2,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=60°,點E是線段AC上一動點,連接DE.請求出![]() 的值及∠EAD的度數(shù);
的值及∠EAD的度數(shù);
(3)拓展延伸
如圖3,在(2)的條件下,取線段DE的中點M,連接AM、BM,若BC=4,則當△ABM是直角三角形時,求線段AD的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
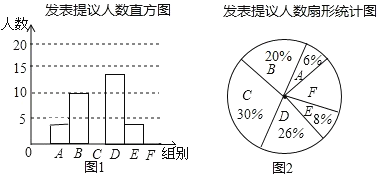
【題目】兩會期間,記者隨機抽取參會的部分代表,對他們某天發(fā)言的次數(shù)進行了統(tǒng)計,其結果如表,并繪制了如圖所示的兩幅不完整的統(tǒng)計圖,請結合圖中相關數(shù)據回答下列問題:
發(fā)言次數(shù)n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得樣本容量為 ,并補全直方圖;
(2)已知A組發(fā)表提議的代表中恰有1位女士,E組發(fā)表提議的代表中只有2位男士,現(xiàn)從A組與E組中分別抽一位代表寫報告,請用列表法或畫樹狀圖的方法,求所抽的兩位代表恰好都是男士的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在近期“抗疫”期間,某藥店銷售A、B兩種型號的口罩,已知銷售800只A型和450只B型的利潤為210元,銷售400只A型和600只B型的利潤為180元.
(1)求每只A型口罩和B型口罩的銷售利潤;
(2)該藥店計劃一次購進兩種型號的口罩共2000只,其中B型口罩的進貨量不超過A型口罩的3倍,設購進A型口罩x只,這2000只口罩的銷售總利潤為y元.
①求y關于x的函數(shù)關系式;
②該藥店購進A型、B型口罩各多少只,才能使銷售總利潤最大?
(3)在銷售時,該藥店開始時將B型口罩提價100%,當收回成本后,為了讓利給消費者,決定把B型口罩的售價調整為進價的15%,求B型口罩降價的幅度.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀下面材料后,解答問題.分母中含有未知數(shù)的不等式叫分式不等式.如:![]() ,
,![]() 等.那么如何求出它們的解集呢?根據我們學過的有理數(shù)除法法則可知,兩數(shù)相除,同號得正,異號得負,其字母表達式為:
等.那么如何求出它們的解集呢?根據我們學過的有理數(shù)除法法則可知,兩數(shù)相除,同號得正,異號得負,其字母表達式為:
(1)若![]() ,
,![]() ,則
,則![]() ,若
,若![]() ,
,![]() ,則
,則![]() ;
;
(2)若![]() ,
,![]() ,則
,則![]() ,若
,若![]() ,
,![]() ,則
,則![]() .反之,(1)若
.反之,(1)若![]() ,則
,則![]() 或
或![]()
(3)若![]() ,則__________或_____________.根據上述規(guī)律,求不等式
,則__________或_____________.根據上述規(guī)律,求不等式![]() ,的解集,方法如下:
,的解集,方法如下:
由上述規(guī)律可知,不等式![]() ,轉化為①
,轉化為①![]() 或②
或②![]()
解不等式組①得![]() ,解不等式組②得
,解不等式組②得![]() .
.
∴不等式![]() ,的解集是
,的解集是![]() 或
或![]() .
.
根據上述材料,解決以下問題:
A、求不等式![]() 的解集
的解集
B、乘法法則與除法法則類似,請你類比上述材料內容,運用乘法法則,解決以下問題:求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
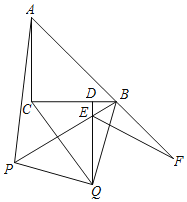
【題目】如圖,已知△ABC中,AC=BC,∠ACB=90°,將△ABC繞點B逆時針方向旋轉得到△PBQ,旋轉角為α,且45°<α<90°.
(1)連接AP,CQ,則![]() = ;
= ;
(2)若QD⊥BC,垂足為點D,∠BQD=15°,QD與PB交于點E,∠BEQ的平分線EF交AB的延長線于點F.
①求旋轉角α的大小;
②求∠F的度數(shù);
③求證:EQ+EB=EF.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某超市銷售一種高檔蔬菜“莼菜”,其進價為16元/kg.經市場調查發(fā)現(xiàn):該商品的日銷售量y(kg)是售價x(元/kg)的一次函數(shù),其售價、日銷售量對應值如表:
售價 | 20 | 30 | 40 |
日銷售量 | 80 | 60 | 40 |
(1)求![]() 關于
關于![]() 的函數(shù)解析式(不要求寫出自變量的取值范圍);
的函數(shù)解析式(不要求寫出自變量的取值范圍);
(2)![]() 為多少時,當天的銷售利潤
為多少時,當天的銷售利潤![]() (元)最大?最大利潤為多少?
(元)最大?最大利潤為多少?
(3)由于產量日漸減少,該商品進價提高了![]() 元/
元/![]() ,物價部門規(guī)定該商品售價不得超過36元/
,物價部門規(guī)定該商品售價不得超過36元/![]() ,該商店在今后的銷售中,日銷售量與售價仍然滿足(1)中的函數(shù)關系.若日銷售最大利潤是864元,求
,該商店在今后的銷售中,日銷售量與售價仍然滿足(1)中的函數(shù)關系.若日銷售最大利潤是864元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
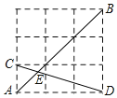
【題目】如圖,在由邊長為1的小正方形組成的網格中.點 A,B,C,D 都在這些小正方形的格點上,AB、CD 相交于點E,則sin∠AEC的值為_____.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com