
【題目】如圖,拋物線y= ![]() x2﹣2x﹣6
x2﹣2x﹣6 ![]() 與x軸交于A,B兩點(點A在點B左側),與y軸交于點C,點D為頂點,點E在拋物線上,且橫坐標為4
與x軸交于A,B兩點(點A在點B左側),與y軸交于點C,點D為頂點,點E在拋物線上,且橫坐標為4 ![]() ,AE與y軸交F.
,AE與y軸交F.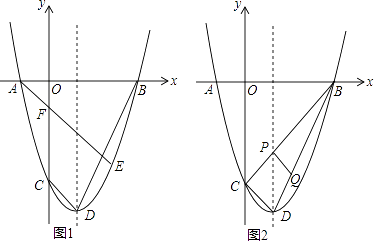
(1)求拋物線的頂點D和F的坐標;
(2)點M,N是拋物線對稱軸上兩點,且M(2 ![]() ,a),N(2
,a),N(2 ![]() ,a+
,a+ ![]() ),是否存在a使F,C,M,N四點所圍成的四邊形周長最小,若存在,求出這個周長最小值,并求出a的值;
),是否存在a使F,C,M,N四點所圍成的四邊形周長最小,若存在,求出這個周長最小值,并求出a的值;
(3)連接BC交對稱軸于點P,點Q是線段BD上的一個動點,自點D以2 ![]() 個單位每秒的速度向終點B運動,連接PQ,將△DPQ沿PQ翻折,點D的對應點為D′,設Q點的運動時間為t(0≤t≤
個單位每秒的速度向終點B運動,連接PQ,將△DPQ沿PQ翻折,點D的對應點為D′,設Q點的運動時間為t(0≤t≤ ![]() )秒,求使得△D′PQ與△PQB重疊部分的面積為△DPQ面積的
)秒,求使得△D′PQ與△PQB重疊部分的面積為△DPQ面積的 ![]() 時對應的t值.
時對應的t值.
【答案】
(1)
解:∵y= ![]() x2﹣2x﹣6
x2﹣2x﹣6 ![]() =
= ![]() (x﹣2
(x﹣2 ![]() )2﹣8
)2﹣8 ![]() ,
,
∴頂點D坐標(2 ![]() ,﹣8
,﹣8 ![]() ),
),
由題意E(4 ![]() ,﹣8
,﹣8 ![]() ),A(﹣2
),A(﹣2 ![]() ,0),B(6
,0),B(6 ![]() ,0),
,0),
設直線AE解析式為y=kx+b,則有 ![]() ,解得
,解得 ![]() ,
,
∴直線AE解析式為y=﹣x﹣2 ![]() ,
,
∴點F坐標(0,﹣2 ![]() )
)
(2)
解:如圖1中,作點F關于對稱軸的對稱點F′,連接FF′交對稱軸于G,在CF上取一點C′,使得CC′= ![]() ,連接C′F′與對稱軸交于點N,此時四邊形CMNF周長最小.
,連接C′F′與對稱軸交于點N,此時四邊形CMNF周長最小.
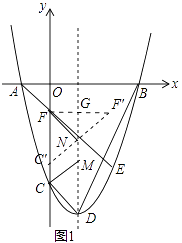
∵四邊形CMNF的周長=CF+NM+CM+FN=5 ![]() +CM+NF,CM+NF=C′N+NF=C′N+NF′=C′F′(兩點之間線段最短),
+CM+NF,CM+NF=C′N+NF=C′N+NF′=C′F′(兩點之間線段最短),
∴此時四邊形CMNF的周長最小.
∵C′F=3 ![]()
∴GN= ![]() C′F=
C′F= ![]() ,
,
∴﹣(a+ ![]() )=2
)=2 ![]() +
+ ![]()
![]() ,
,
∴a=﹣ ![]() ,
,
∵C′F′= ![]() =5
=5 ![]() ,
,
∴四邊形CMNF的周長最小值=5 ![]() +5
+5 ![]() =10
=10 ![]()
(3)
解:如圖2中,作PF⊥BD于F,QH⊥對稱軸于H.
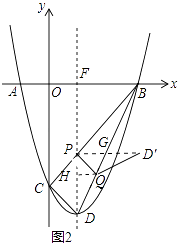
由題意可知BD= ![]() =4
=4 ![]() ,DQ=2
,DQ=2 ![]() t,
t,
∵S△PQG= ![]() S△DPQ=
S△DPQ= ![]() S△PD′Q,
S△PD′Q,
∴PG= ![]() PD′=
PD′= ![]() PD=2
PD=2 ![]() =
= ![]() BF,
BF,
情形①PG∥FB時,∵PF=PD,
∴BG=GD,
∴PG= ![]() BF=2
BF=2 ![]() ,
,
在Rt△QHD中,sin∠HDQ= ![]() ,DQ=2
,DQ=2 ![]() t,
t,
∴HQ=2 ![]() t,HD=4
t,HD=4 ![]() t,
t,
∵∠QPD′=∠QPD=45°,
∴PH=HQ=2 ![]() t,
t,
∴PH+HD=PD,
∴6 ![]() t=4
t=4 ![]() ,
,
∴t= ![]() .
.
情形②如圖3中,PG′=PG=2 ![]() ,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.
,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.
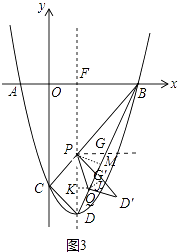
由sin∠PDG=sin∠GPM= ![]() =
= ![]() ,
,
∴MG′=MG= ![]() ,
,
∴G′D=BD﹣GG′= ![]() ,
,
∵ ![]() =
= ![]() =
= 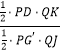 ,
,
∵∠QPD=∠QPG′,QK⊥PD,QJ⊥PG′,
∴QK=QJ,
∴ ![]() =
= ![]() =2,
=2,
∴QD= ![]() ×
× ![]() =
= ![]() ,
,
∴t= ![]() =
= ![]() ,
,
綜上所述t= ![]() 或
或 ![]() 秒時,△D′PQ與△PQB重疊部分的面積為△DPQ面積的
秒時,△D′PQ與△PQB重疊部分的面積為△DPQ面積的 ![]()
【解析】(1)利用配方法或公式法求頂點坐標,求出最小AE即可求出點F坐標.(2)如圖1中,作點F關于對稱軸的對稱點F′,連接FF′交對稱軸于G,在CF上取一點C′,使得CC′= ![]() ,連接C′F′與對稱軸交于點N,此時四邊形CMNF周長最小.(3)分兩種情形①PG∥FB時;②如圖3中,PG′=PG=2
,連接C′F′與對稱軸交于點N,此時四邊形CMNF周長最小.(3)分兩種情形①PG∥FB時;②如圖3中,PG′=PG=2 ![]() ,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.分別求解即可.
,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.分別求解即可.
【考點精析】通過靈活運用二次函數的圖象,掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點即可以解答此題.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:初中數學 來源: 題型:
【題目】下列各式中:
①由3x=﹣4系數化為1得x=﹣![]() ;
;
②由5=2﹣x移項得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括號得4x﹣2﹣3x﹣9=1.
其中正確的個數有( )
A. 0個 B. 1個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,點F為BE中點,連接DF,CF. 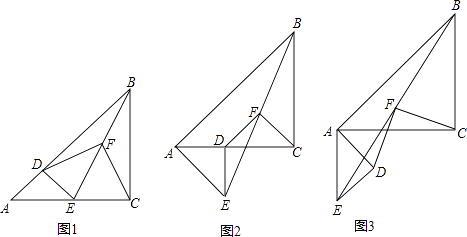
(1)如圖1,當點D在AB上,點E在AC上,請直接寫出此時線段DF,CF的數量關系和位置關系(不用證明); 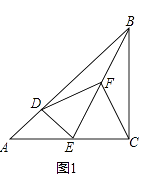
(2)如圖2,在(1)的條件下將△ADE繞點A順時針旋轉45°時,請你判斷此時(1)中的結論是否仍然成立,并證明你的判斷; 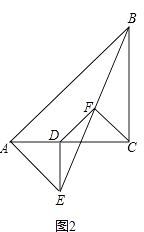
(3)如圖3,在(1)的條件下將△ADE繞點A順時針旋轉90°時,若AD=1,AC= ![]() ,求此時線段CF的長(直接寫出結果).
,求此時線段CF的長(直接寫出結果). 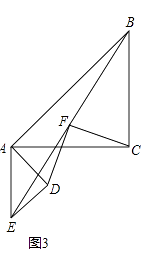
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,過點B(6,0)的直線AB與直線OA相交于點A(4,2),動點M沿路線O→A→C運動.
(1)求直線AB的解析式.
(2)求△OAC的面積.
(3)當△OMC的面積是△OAC的面積的![]() 時,求出這時點M的坐標.
時,求出這時點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐵路貨運調度站有A、B兩個信號燈,在燈這旁停靠著甲、乙、丙三列火車.它們中最長的車長與居中車長之差等于居中車長與最短車長之差,其中乙車的車長居中,最開始的時候,甲、丙兩車車尾對齊,且車尾正好位于A信號燈處,而車頭則沖著B信號燈的方向,乙車的車尾則位于B信號燈處,車頭則沖著A的方向,現在,三列火車同時出發向前行駛,3秒之后三列火車的車頭恰好相遇,再過9秒,甲車恰好超過丙車,而丙車也正好完全和乙車錯開,請問:甲乙兩車從車頭相遇直到完全錯開一共用了_____秒鐘.
查看答案和解析>>
科目:初中數學 來源: 題型:
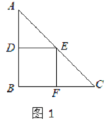
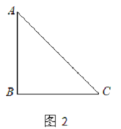
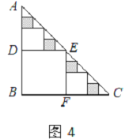
【題目】已知:△ABC是一張等腰直角三角形紙板,∠B=90°,AB=BC=1.
(1)要在這張紙板上剪出一個正方形,使這個正方形的四個頂點都在△ABC的邊上.小林設計出了一種剪法,如圖1所示.請你再設計出一種不同于圖1的剪法,并在圖2中畫出來.
(2)若按照小林設計的圖1所示的剪法來進行裁剪,記圖1為第一次裁剪,得到1個正方形,將它的面積記為![]() ,則
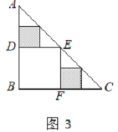
,則![]() =___________;在余下的2個三角形中還按照小林設計的剪法進行第二次裁剪(如圖3),得到2個新的正方形,將此次所得2個正方形的面積的和記為
=___________;在余下的2個三角形中還按照小林設計的剪法進行第二次裁剪(如圖3),得到2個新的正方形,將此次所得2個正方形的面積的和記為![]() ,則
,則![]() =___________;在余下的4個三角形中再按照小林設計的的剪法進行第三次裁剪(如圖4),得到4個新的正方形,將此次所得4個正方形的面積的和記為
=___________;在余下的4個三角形中再按照小林設計的的剪法進行第三次裁剪(如圖4),得到4個新的正方形,將此次所得4個正方形的面積的和記為![]() ;按照同樣的方法繼續操作下去……,第
;按照同樣的方法繼續操作下去……,第![]() 次裁剪得到_________個新的正方形,它們的面積的和
次裁剪得到_________個新的正方形,它們的面積的和![]() =______________.
=______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com