
【題目】某中學組織學生去福利院慰問,在準備禮品時發現,購買1個甲禮品比購買1個乙禮品多花40元,并且花費600元購買甲禮品和花費360元購買乙禮品的數量相等.
(1)求甲、乙兩種禮品的單價各為多少元?
(2)學校準備購買甲、乙兩種禮品共30個送給福利院的老人,要求購買禮品的總費用不超過2000元,那么最多可購買多少個甲禮品?
【答案】
(1)
解:設購買一個乙禮品需要x元,根據題意得:
![]() =
=![]() ,
,
解得:x=60,
經檢驗x=60是原方程的根,
∴x+40=100.
答:甲禮品100元,乙禮品60元;
(2)
解:設總費用不超過2000元,可購買m個甲禮品,則購買乙禮品(30﹣m)個,
根據題意得:100m+60(30﹣m)≤2000,
解得:m≤5.
答:最多可購買5個甲禮品.
【解析】(1)設購買一個乙禮品需要x元,根據“花費600元購買甲禮品和花費360元購買乙禮品的數量相等”列分式方程求解即可;
(2)設總費用不超過2000元,可購買m個甲禮品,則購買乙禮品(30﹣m)個,根據題意列不等式求解即可.
【考點精析】本題主要考查了分式方程的應用的相關知識點,需要掌握列分式方程解應用題的步驟:審題、設未知數、找相等關系列方程、解方程并驗根、寫出答案(要有單位)才能正確解答此題.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊長為2,∠DAB=60°,E為BC的中點,在對角線AC上存在一點P,使△PBE的周長最小,則△PBE的周長的最小值為 . 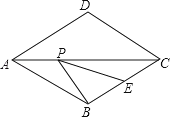
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點D,E分別是邊BC,AC的中點,連接DE,AD,點F在BA的延長線上,且AF=![]() AB,連接EF,判斷四邊形ADEF的形狀,并加以證明.
AB,連接EF,判斷四邊形ADEF的形狀,并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD的對角線AC、BD相交于點O,EF、GH過點O,且點E、H在邊AB上,點G、F在邊CD上,向ABCD內部投擲飛鏢(每次均落在ABCD內,且落在ABCD內任何一點的機會均等)恰好落在陰影區域的概率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,△ABC在平面直角坐標系中的位置如圖①所示,A點坐標為(﹣6,0),B點坐標為(4,0),點D為BC的中點,點E為線段AB上一動點,連接DE經過點A、B、C三點的拋物線的解析式為y=ax2+bx+8.
(1)求拋物線的解析式;
(2)如圖①,將△BDE以DE為軸翻折,點B的對稱點為點G,當點G恰好落在拋物線的對稱軸上時,求G點的坐標;
(3)如圖②,當點E在線段AB上運動時,拋物線y=ax2+bx+8的對稱軸上是否存在點F,使得以C、D、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,![]() , 連接ED、BD,延長AE交BD的延長線于點M,過點D作⊙O的切線交AB的延長線于點C.
, 連接ED、BD,延長AE交BD的延長線于點M,過點D作⊙O的切線交AB的延長線于點C.
(1)若OA=CD=![]() ,求陰影部分的面積;
,求陰影部分的面積;
(2)求證:DE=DM.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y=x+m與拋物線x2=4y相切,且與x軸的交點為M,點N(﹣1,0).若動點P與兩定點M,N所構成三角形的周長為6.
(Ⅰ)求動點P的軌跡C的方程;
(Ⅱ) 設斜率為 ![]() 的直線l交曲線C于A,B兩點,當PN⊥MN時,證明:∠APN=∠BPN.
的直線l交曲線C于A,B兩點,當PN⊥MN時,證明:∠APN=∠BPN.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AC∥BD,AB和CD相交于點E,AC=6,BD=4,F是BC上一點,S△BEF:S△EFC=2:3. 
(1)求EF的長;
(2)如果△BEF的面積為4,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com