
 如圖,在△ABC中,BD⊥AC,垂足為D,AB=AC=9,BC=6,求BD的長.
如圖,在△ABC中,BD⊥AC,垂足為D,AB=AC=9,BC=6,求BD的長. 分析 作AE⊥BC于E,由等腰三角形的性質得出BE=CE=$\frac{1}{2}$BC=3,由勾股定理求出AE,證明△AEC∽△BDC,得出對應邊成比例,即可求出BD的長.
解答 解:作AE⊥BC于E,如圖所示:
則∠AEC=90°,
∵AB=AC,
∴BE=CE=$\frac{1}{2}$BC=3,
∴AE=$\sqrt{{9}^{2}-{3}^{2}}$=6$\sqrt{2}$,
∵BD⊥AC,
∴∠BDC=90°=∠AEC,
又∵∠C=∠C,
∴△AEC∽△BDC,
∴AE:BD=AC:BC,
∴BD=$\frac{AE•BC}{AC}$=$\frac{6\sqrt{2}×6}{9}$=4$\sqrt{2}$.
點評 此題考查了勾股定理、等腰三角形的性質、相似三角形的判定與性質;熟練掌握等腰三角形的性質和勾股定理,證明三角形相似是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
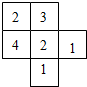 如圖所示是由若干個大小相同的小立方體所組成幾何體從上面看的圖,小正方形中的數字表示在該位置的小立方體的個數,請畫出這個幾何體從正面看到的圖,從左面看到的圖.
如圖所示是由若干個大小相同的小立方體所組成幾何體從上面看的圖,小正方形中的數字表示在該位置的小立方體的個數,請畫出這個幾何體從正面看到的圖,從左面看到的圖.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
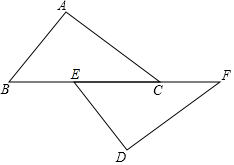 如圖,已知點B、E、C、F在一條直線上,AC∥DE,AC=DE,∠A=∠D.
如圖,已知點B、E、C、F在一條直線上,AC∥DE,AC=DE,∠A=∠D.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
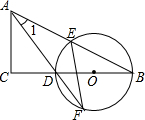 如圖,△ABC中,∠C=90°,D是BC邊上一點,以DB為直徑的⊙O交AB于E,交AD的延長線于F,連結EF,∠1=∠F.
如圖,△ABC中,∠C=90°,D是BC邊上一點,以DB為直徑的⊙O交AB于E,交AD的延長線于F,連結EF,∠1=∠F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC的頂點坐標分別為A(4,4),B(2,1),C(5,1).
如圖,△ABC的頂點坐標分別為A(4,4),B(2,1),C(5,1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
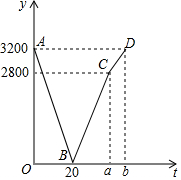 已知甲、乙兩地相距3200m,小王、小李分別從甲、乙兩地同時出發,相向而行,兩人相遇后立即返回到各自的出發地并停止行進.已知小李的速度始終是60m/min,小王在相遇后以勻速返回,但比小李晚回到原地.在整個行進過程中,他們之間的距離y(m)與行進的時間t(min)之間的函數關系如圖中的折線段AB-BC-CD所示,請結合圖象信息解答下列問題:
已知甲、乙兩地相距3200m,小王、小李分別從甲、乙兩地同時出發,相向而行,兩人相遇后立即返回到各自的出發地并停止行進.已知小李的速度始終是60m/min,小王在相遇后以勻速返回,但比小李晚回到原地.在整個行進過程中,他們之間的距離y(m)與行進的時間t(min)之間的函數關系如圖中的折線段AB-BC-CD所示,請結合圖象信息解答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com