
分析 (1)如圖1中,連接OF、OE、GB、FB,作GM⊥OB于M,FN⊥OB于N.只要證明△OBG∽△OAB,可得點F是自相似點,△FOB∽△BAO,可得點F是自相似點.
(2)①如圖2,過點M作MG⊥x軸于G點.由△P1ON∽△NOM,△MP2N∽△MNO,推出∠OP1N=∠MNO=120°,∠MP2N=∠MNO=120°,推出∠NP1P2=∠NP2P1=60°,推出△NP1P2是等邊三角形,推出OP1=P1P2=P2M,推出P1的橫坐標為1,P2的橫坐標為2,代入y=$\frac{\sqrt{3}}{3}$x,即可解決問題.
②以O為圓心2為半徑作圓交反比例函數于M1,M2,以N為圓心2為半徑作圓交反比例函數的圖象于M3,M4.滿足條件的點M有4個.
解答 解:(1)如圖1中,連接OF、OE、GB、FB,作GM⊥OB于M,FN⊥OB于N.
由題意可知點G在OA上,
∵tan∠AOB=$\frac{AB}{OB}$=$\sqrt{3}$,
∴∠AOB=60°,
∵tan∠GBM=$\frac{GM}{BM}$=$\frac{\frac{\sqrt{3}}{2}}{\frac{3}{2}}$=$\frac{\sqrt{3}}{3}$,
∴∠OBG=30°,
∴∠BOG=∠AOB,∠OBG=∠A,
∴△OBG∽△OAB,
∴點F是自相似點,
同理可得∠FON=∠A=30°,∠FBO=∠AOB=60°,
∴△FOB∽△BAO,
∴點F是自相似點,
故答案為F,G.
(2)①如圖2,過點M作MG⊥x軸于G點.
∵M點的橫坐標為3,
∴y=$\frac{3\sqrt{3}}{3}$=$\sqrt{3}$,
∴M(3,$\sqrt{3}$),
∴OM=2$\sqrt{3}$,∠MON=∠NMO=30°,∠ONM=120°,
直線OM的表達式為y=$\frac{\sqrt{3}}{3}$,
在Rt△MHG中,∠MGN=90°,MN2=MG2+NG2,
設NM=NO=m,則NG=3-m,
∴m2=(3-m)2+($\sqrt{3}$)2,
∴ON=MN=m=2,
∵△P1ON∽△NOM,△MP2N∽△MNO,
∴∠OP1N=∠MNO=120°,∠MP2N=∠MNO=120°,
∴∠NP1P2=∠NP2P1=60°,
∴△NP1P2是等邊三角形,
∴OP1=P1P2=P2M,
∴P1的橫坐標為1,P2的橫坐標為2,代入y=$\frac{\sqrt{3}}{3}$x,
可得P1(1,$\frac{\sqrt{3}}{3}$),P2(2,$\frac{2\sqrt{3}}{3}$)
綜上所述,P點坐標為(1,$\frac{\sqrt{3}}{3}$))或(2,$\frac{2\sqrt{3}}{3}$).
②如圖3中,滿足條件的點M有4個.
以O為圓心2為半徑作圓交反比例函數于M1,M2,以N為圓心2為半徑作圓交反比例函數的圖象于M3,M4.
故答案為4.
點評 本題考查反比例函數綜合題、相似三角形的判定和性質、一次函數的應用、等腰三角形的性質和判定等知識,解題的關鍵是理解題意,靈活運用所學知識解決問題,屬于中考壓軸題.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源: 題型:解答題
 如圖,△ABC的頂點坐標分別為A(4,4),B(2,1),C(5,1).
如圖,△ABC的頂點坐標分別為A(4,4),B(2,1),C(5,1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
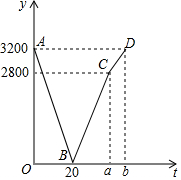 已知甲、乙兩地相距3200m,小王、小李分別從甲、乙兩地同時出發,相向而行,兩人相遇后立即返回到各自的出發地并停止行進.已知小李的速度始終是60m/min,小王在相遇后以勻速返回,但比小李晚回到原地.在整個行進過程中,他們之間的距離y(m)與行進的時間t(min)之間的函數關系如圖中的折線段AB-BC-CD所示,請結合圖象信息解答下列問題:
已知甲、乙兩地相距3200m,小王、小李分別從甲、乙兩地同時出發,相向而行,兩人相遇后立即返回到各自的出發地并停止行進.已知小李的速度始終是60m/min,小王在相遇后以勻速返回,但比小李晚回到原地.在整個行進過程中,他們之間的距離y(m)與行進的時間t(min)之間的函數關系如圖中的折線段AB-BC-CD所示,請結合圖象信息解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,四點A、B、C、D,按照下列語句畫出圖形;
如圖,四點A、B、C、D,按照下列語句畫出圖形;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com