
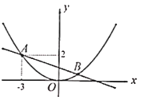
【題目】已知二次函數圖象的頂點在原點![]() ,對稱軸為
,對稱軸為![]() 軸.直線
軸.直線![]() 的圖象與二次函數的圖象交于點
的圖象與二次函數的圖象交于點![]() 和點
和點![]() (點
(點![]() 在點
在點![]() 的左側)
的左側)
(1)求![]() 的值及直線
的值及直線![]() 解析式;
解析式;
(2)若過點![]() 的直線
的直線![]() 平行于直線
平行于直線![]() 且直線
且直線![]() 與二次函數圖象只有一個交點
與二次函數圖象只有一個交點![]() ,求交點
,求交點![]() 的坐標.
的坐標.
【答案】(1)m=![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)由于拋物線的頂點為原點,因此可設其解析式為y=ax2,直接將A點,B點的坐標代入拋物線中即可求出拋物線的解析式以及m的值,進而可知出點B的坐標,再將A,B點的坐標代入一次函數中,即可求出一次函數的解析式.
(2)根據題意可知直線l2的解析式![]() ,由拋物線與l2只有一個交點,聯立直線
,由拋物線與l2只有一個交點,聯立直線![]() 與二次函數的解析式,消去y,得出一個含x一元二次方程,根據方程的判別式為0可求得n的值,進而得出結果.
與二次函數的解析式,消去y,得出一個含x一元二次方程,根據方程的判別式為0可求得n的值,進而得出結果.
(1)解:假設二次函數的解析式為![]() ,
,
將![]() 分別代入二次函數的解析式
分別代入二次函數的解析式![]() ,
,
得: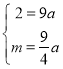 ,解得
,解得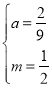 .
.
解得:![]() .
.
![]() 將
將![]() 代入
代入![]() 中,
中,
得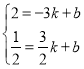 ,,解得:
,,解得: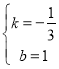 .
.
![]() 的解析式為
的解析式為![]() .
.
(2)由題意可知:l2∥l1,
可設直線![]() 的解析式為:
的解析式為:![]()
![]() 過點
過點![]() ,則有:
,則有:![]() .
.
![]() .
.
由題意,聯立直線![]() 與二次函數的解析式,可得以下方程組:
與二次函數的解析式,可得以下方程組:
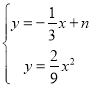 ,
,
消元,得:![]() ,
,
整理,得:![]() , ①
, ①
由題意,得![]() 與
與![]() 只有一個交點,
只有一個交點,
可得:![]() ,
,
解得:![]() .
.
將![]() 代回方程①中,得
代回方程①中,得![]() .
.
將![]() 代入
代入![]() 中,
中,
得![]() .
.
可得交點![]() 坐標為
坐標為![]() .
.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:初中數學 來源: 題型:
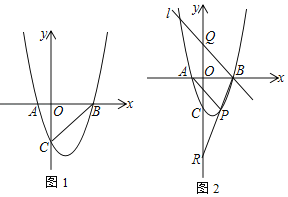
【題目】如圖1,在平面直角坐標系中,拋物線y=ax2﹣2x﹣3a與x軸交于A、B兩點,與y軸交于C點,OC=OB,點P為拋物線上一動點
(1)求拋物線的解析式;
(2)當點P運動到拋物線對稱軸右側時如圖2,連PC、BC、BP得△BCP.設△BCP的面積為s,點P的橫坐標為x.若s<![]() ,求x的取值范圍;
,求x的取值范圍;
(3)當點P運動到第四象限時,連AP、BP,BP交y軸于點R,過B作直線l∥AP交y軸于點Q,問:QR、OC之間是否存在確定的數量關系?若存在,請求出并證明;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
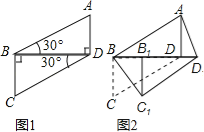
【題目】將兩塊全等的含30°角的三角尺如圖1擺放在一起,設較短直角邊為1,如圖2,將Rt△BCD沿射線BD方向平移,在平移的過程中,當點B的移動距離為 時,四邊ABC1D1為矩形;當點B的移動距離為 時,四邊形ABC1D1為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
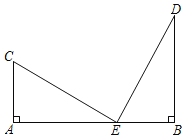
【題目】如圖,已知BD⊥AB于點B,AC⊥AB于點A,且BD=3,AC=2,AB=m,在線段AB上找一點E,使△BDE與△ACE相似,若這樣的點E有且只有兩個,則m的值是______
查看答案和解析>>
科目:初中數學 來源: 題型:
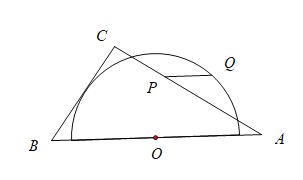
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以邊
,以邊![]() 的中點
的中點![]() 為圓心作半圓,使
為圓心作半圓,使![]() 與半圓相切,點
與半圓相切,點![]() 分別是邊
分別是邊![]() 和半圓上的動點,連接
和半圓上的動點,連接![]() ,則
,則![]() 長的最大值與最小值的和是( )
長的最大值與最小值的和是( )
A.8B.9C.10D.12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級(1)班的小華和小紅兩名學生10次數學測試成績如下表(表I)所示:
小花 | 70 | 80 | 90 | 80 | 70 | 90 | 80 | 100 | 60 | 80 |
小紅 | 90 | 80 | 100 | 60 | 90 | 80 | 90 | 60 | 60 | 90 |
現根據上表數據進行統計得到下表(表Ⅱ):
姓名 | 平均成績 | 中位數 | 眾數 |
小華 | 80 | ||
小紅 | 80 | 90 |
(1)填空:根據表I的數據完成表Ⅱ中所缺的數據;
(2)老師計算了小紅的方差![]() 請你計算小華的方差并說明哪名學生的成績較為穩定.
請你計算小華的方差并說明哪名學生的成績較為穩定.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一艘輪船從位于燈塔C的北偏東60°方向,距離燈塔60 n mile的小島A出發,沿正南方向航行一段時間后,到達位于燈塔C的南偏東45°方向上的B處,這時輪船B與小島A的距離是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某玩具商店以每件60元為成本購進一批新型玩具,以每件100元的價格銷售則每天可賣出20件,為了擴大銷售,增加盈利,盡快減少庫存,商店決定采取適當的降價措施,經調查發現:若每件玩具每降價1元,則每天可多賣2件.
(1)若商店打算每天盈利1200元,每件玩具的售價應定為多少元?
(2)若商店為追求效益最大化,每件玩具的售價定為多少元時,商店每天盈利最多?最多盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】手機微信推出了紅包游戲,它有多種玩法,其中一種為“拼手氣紅包”,用戶設好總金額以及紅包個數后,可以生成不等金額的紅包,現有一用戶發了三個“拼手氣紅包”,總金額為3元,隨機被甲、乙、丙三人搶到.
(1)下列事件中,確定事件是 ,①丙搶到金額為1元的紅包;②乙搶到金額為4元的紅包;③甲、乙兩人搶到的紅包金額之和一定比丙搶到的紅包金額多
(2)記金額最多、居中、最少的紅包分別為A,B,C.求甲搶到紅包A,乙搶到紅包C的概率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com