
【題目】拋物線![]() 的圖像與
的圖像與![]() 軸的一個(gè)交點(diǎn)為
軸的一個(gè)交點(diǎn)為![]() ,另一交點(diǎn)為
,另一交點(diǎn)為![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,對稱軸是直線
,對稱軸是直線![]() .
.
(1)求該二次函數(shù)的表達(dá)式及頂點(diǎn)坐標(biāo);
(2)畫出此二次函數(shù)的大致圖象;利用圖象回答:當(dāng)![]() 取何值時(shí),
取何值時(shí),![]() ?
?
(3)若點(diǎn)![]() 在拋物線
在拋物線![]() 的圖像上,且點(diǎn)
的圖像上,且點(diǎn)![]() 到
到![]() 軸距離小于3,則
軸距離小于3,則![]() 的取值范圍為 ;
的取值范圍為 ;

【答案】(1)![]() ,
,![]() ;(2)見解析,
;(2)見解析,![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根據(jù)圖像對稱軸是直線![]() ,得到
,得到![]() ,再將
,再將![]() ,
, ![]() 代入解析式,得到關(guān)于a、b、c的方程組,即可求得系數(shù),得到解析式,再求出頂點(diǎn)坐標(biāo)即可;
代入解析式,得到關(guān)于a、b、c的方程組,即可求得系數(shù),得到解析式,再求出頂點(diǎn)坐標(biāo)即可;
(2)根據(jù)特定點(diǎn)畫出二次函數(shù)的大致圖象,根據(jù)二次函數(shù)與不等式的關(guān)系,即可得到![]() 對應(yīng)的x的取值范圍.
對應(yīng)的x的取值范圍.
(3)求出當(dāng)![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 時(shí),y的值,即可求出
時(shí),y的值,即可求出![]() 的取值范圍.
的取值范圍.
(1)因?yàn)閳D像對稱軸是直線![]() ,所以
,所以![]() ,
,
將![]() ,
, ![]() 代入解析式,得:由題知
代入解析式,得:由題知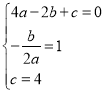 ,解得
,解得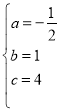 ,所以解析式為:
,所以解析式為:![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,所以頂點(diǎn)坐標(biāo)
,所以頂點(diǎn)坐標(biāo)![]() .
.
(2)二次函數(shù)的大致圖象:

當(dāng)![]() 或
或![]() ,
,![]() .
.
(3)當(dāng)![]() 時(shí),得
時(shí),得![]() ,當(dāng)
,當(dāng)![]() 時(shí),得
時(shí),得![]() ,
,
所以y取值范圍為![]() ,即
,即![]() 的取值范圍為
的取值范圍為![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
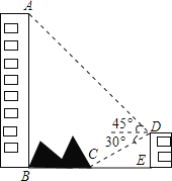
【題目】 如圖,大樓AB右側(cè)有一障礙物,在障礙物的旁邊有一幢小樓DE,在小樓的頂端D處測得障礙物邊緣點(diǎn)C的俯角為30°,測得大樓頂端A的仰角為45°(點(diǎn)B,C,E在同一水平直線上),已知AB=80m,DE=10m,求障礙物B,C兩點(diǎn)間的距離(結(jié)果精確到0.1m)(參考數(shù)據(jù):![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在甲、乙兩個(gè)不透明的布袋里,都裝有3個(gè)大小、材質(zhì)完全相同的小球,其中甲袋中的小球上分別標(biāo)有數(shù)字0,1,2,乙袋中的小球上分別標(biāo)有數(shù)字﹣1,﹣2,3,現(xiàn)從甲袋中任意摸出一個(gè)小球,記其標(biāo)有的數(shù)字為x,再從乙袋中任意摸出一個(gè)小球,記其標(biāo)有的數(shù)字為y,以此確定點(diǎn)M的坐標(biāo)(x,y).
(1)請你用畫樹狀圖或列表的方法,寫出點(diǎn)M的所有可能的坐標(biāo);
(2)求點(diǎn)M(x,y)在函數(shù)y=﹣![]() 的圖象上的概率.
的圖象上的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】綜合與探究:
如圖,將拋物線![]() 向右平移
向右平移![]() 個(gè)單位長度,再向下平移
個(gè)單位長度,再向下平移![]() 個(gè)單位長度后,得到的拋物線
個(gè)單位長度后,得到的拋物線![]() ,平移后的拋物線
,平移后的拋物線![]() 與
與![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .拋物線
.拋物線![]() 的對稱軸
的對稱軸![]() 與拋物線
與拋物線![]() 交于點(diǎn)
交于點(diǎn)![]() .
.

(1)請你直接寫出拋物線![]() 的解析式;(寫出頂點(diǎn)式即可)
的解析式;(寫出頂點(diǎn)式即可)
(2)求出![]() ,
,![]() ,
,![]() 三點(diǎn)的坐標(biāo);
三點(diǎn)的坐標(biāo);
(3)在![]() 軸上存在一點(diǎn)
軸上存在一點(diǎn)![]() ,使
,使![]() 的值最小,求點(diǎn)
的值最小,求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,△ABC中,AB=AC,點(diǎn)F在邊BC上

(1)如圖1,AF=BF,求證:AB2=BFBC;
(2)如圖2,FC=2BF,點(diǎn)E、M在直線AB上,EF∥AC,cosB=n,且FM2=MEMB
①若M在邊AB上,求![]() 的值(用含n的式子表示);
的值(用含n的式子表示);
②若M在BA的延長線上時(shí),直接寫出n的范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
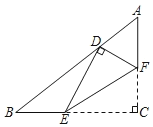
【題目】如圖,在Rt△ABC中,∠C=90°,AB=5,BC=4,點(diǎn)E,F分別在邊BC,AC上,沿EF所在的直線折疊∠C,使點(diǎn)C的對應(yīng)點(diǎn)D恰好落在邊AB上,若△EFC和△ABC相似,則BD的長為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
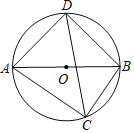
【題目】如圖,![]() 是⊙
是⊙![]() 的直徑,點(diǎn)
的直徑,點(diǎn)![]() 分別在兩個(gè)半圓上(不與點(diǎn)
分別在兩個(gè)半圓上(不與點(diǎn)![]() 重合),
重合),![]() 的長分別是關(guān)于
的長分別是關(guān)于![]() 的方程
的方程![]()
![]() 的兩個(gè)實(shí)數(shù)根.
的兩個(gè)實(shí)數(shù)根.
(1)![]() 的值為_____;
的值為_____;
(2)連接![]() 三者之間的等量關(guān)系為_____.
三者之間的等量關(guān)系為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】綜合與實(shí)踐
在數(shù)學(xué)活動課上,老師出示了這樣一個(gè)問題:如圖1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 邊上的任意一點(diǎn).將
邊上的任意一點(diǎn).將![]() 沿過點(diǎn)
沿過點(diǎn)![]() 的直線折疊,使點(diǎn)
的直線折疊,使點(diǎn)![]() 落在斜邊
落在斜邊![]() 上的點(diǎn)
上的點(diǎn)![]() 處.問是否存在
處.問是否存在![]() 是直角三角形?若不存在,請說明理由;若存在,求出此時(shí)
是直角三角形?若不存在,請說明理由;若存在,求出此時(shí)![]() 的長度.
的長度.

探究展示:勤奮小組很快找到了點(diǎn)![]() 、
、![]() 的位置.
的位置.
如圖2,作![]() 的角平分線交
的角平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,此時(shí)
,此時(shí)![]() 沿
沿![]() 所在的直線折疊,點(diǎn)
所在的直線折疊,點(diǎn)![]() 恰好在
恰好在![]() 上,且
上,且![]() ,所以
,所以![]() 是直角三角形.
是直角三角形.
問題解決:
(1)按勤奮小組的這種折疊方式,![]() 的長度為 .
的長度為 .
(2/span>)創(chuàng)新小組看完勤奮小組的折疊方法后,發(fā)現(xiàn)還有另一種折疊方法,請?jiān)趫D3中畫出來.
(3)在(2)的條件下,求出![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】圖1是某浴室花灑實(shí)景圖,圖2是該花灑的側(cè)面示意圖.已知活動調(diào)節(jié)點(diǎn)B可以上下調(diào)整高度,離地面CD的距離BC=160cm.設(shè)花灑臂與墻面的夾角為α,可以扭動花灑臂調(diào)整角度,且花灑臂長AB=30cm.假設(shè)水柱AE垂直AB直線噴射,小華在離墻面距離CD=120cm處淋浴.

(1)當(dāng)α=30°時(shí),水柱正好落在小華的頭頂上,求小華的身高DE.
(2)如果小華要洗腳,需要調(diào)整水柱AE,使點(diǎn)E與點(diǎn)D重合,調(diào)整的方式有兩種:
①其他條件不變,只要把活動調(diào)節(jié)點(diǎn)B向下移動即可,移動的距離BF與小華的身高DE有什么數(shù)量關(guān)系?直接寫出你的結(jié)論;
②活動調(diào)節(jié)點(diǎn)B不動,只要調(diào)整α的大小,在圖3中,試求α的度數(shù).
(參考數(shù)據(jù):![]() ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com