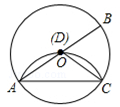
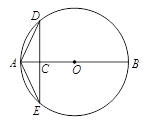
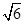在⊙O中,AB為直徑,點C為圓上一點,將劣弧沿弦AC翻折交AB于點D,連結CD.如圖,若點D與圓心O重合,AC=2,求⊙O的半徑r;
⊙O的半徑r為

.
試題分析:過點O作OE⊥AC于E,根據(jù)垂徑定理可得AE=

AC,再根據(jù)翻折的性質可得OE=

r,然后在Rt△AOE中,利用勾股定理列式計算即可得解.
試題解析:如圖,過點O作OE⊥AC于E,

則AE=

AC=

×2=1,
∵翻折后點D與圓心O重合,
∴OE=

r,
在Rt△AOE中,AO
2=AE
2+OE
2,
即r
2=1
2+(

r)
2,
解得r=

.
故⊙O的半徑r為

.
練習冊系列答案
相關習題
科目:初中數(shù)學
來源:不詳
題型:解答題
如圖,已知AB,AC分別是⊙O的直徑和弦,點G為
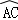
上一點,GE⊥AB,垂足為點E,交AC于點D,過點C的切線與AB的延長線交于點F,與EG的延長線交于點P,連接AG.
(1)求證:△PCD是等腰三角形;
(2)若點D為AC的中點,且∠F=30°,BF=2,求△PCD的周長和AG的長.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
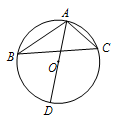
如圖,△ABC的3個頂點都在⊙O上,⊙O的直徑AD=2,∠ABC=30°,則AC的長度為
.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
如圖,AB是⊙O的直徑,AC是弦,直線EF經(jīng)過點C,AD⊥EF于點D,∠DAC=∠BAC.
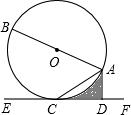
(1)求證:EF是⊙O的切線;
(2)求證:AC
2=AD•AB;
(3)若⊙O的半徑為2,∠ACD=30°,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
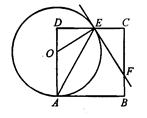
如圖,點O在邊長為8的正方形ABCD的AD邊上運動(4<C)A<8),以O為圓心,OA長為半徑作圓,交CD于點E,連接OE、AE,過點E作直線EF交BC于 點F,且∠CEF=2∠DAE.
(1)求證:直線EF為⊙O的切線;
(2)在點O的運動過程中,設DE=x,解決下列問題:
①求OD·CF的最大值,并求此時半徑的長;
②試猜想并證明△CEF的周長為定值.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
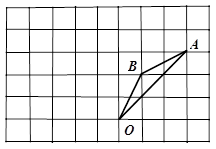
如圖,在邊長為1的正方形組成的網(wǎng)格中,△AOB的頂點均在格點上,點A,B的坐標分別是A(3,3)、B(1,2),△AOB繞點O逆時針旋轉90°后得到△
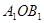
.
(1)畫出△
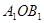
,直接寫出點
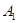
,
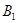
的坐標;
(2)在旋轉過程中,點B經(jīng)過的路徑的長;
(3)求在旋轉過程中,線段AB所掃過的面積.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:單選題
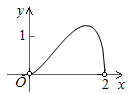
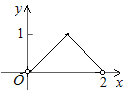
如圖,點C為⊙O的直徑AB上一動點,AB=2,過點C作DE⊥AB交⊙O于點D、E,連結AD,AE. 當點C在AB上運動時,設AC的長為x,△ADE的面積為y,下列圖象中,能表示y與x的函數(shù)關系的圖象大致是( )
A.
B.
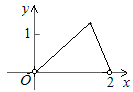
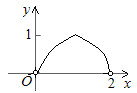
C.
D.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:單選題
如圖,⊙O與Rt△ABC的斜邊AB相切于點D,與直角邊AC相交于點E,且DE∥BC.已知AE=2
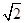
,AC=3
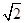
,BC=6,則⊙O的半徑是
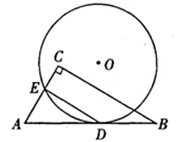
A.3 B.2
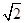
C.2
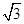
D.
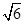
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
如圖,圓錐底面半徑OA=10㎝,母線PA=30㎝.由底面周長上一點A出發(fā)繞其側面一周的最短路線長度是多少?
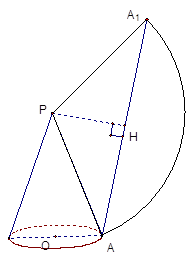
查看答案和解析>>


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案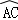 上一點,GE⊥AB,垂足為點E,交AC于點D,過點C的切線與AB的延長線交于點F,與EG的延長線交于點P,連接AG.
上一點,GE⊥AB,垂足為點E,交AC于點D,過點C的切線與AB的延長線交于點F,與EG的延長線交于點P,連接AG.


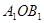 .
.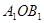 ,直接寫出點
,直接寫出點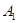 ,
, 的坐標;
的坐標;

 B.
B.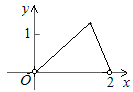 C.
C. D.
D.
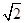 ,AC=3
,AC=3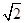 ,BC=6,則⊙O的半徑是
,BC=6,則⊙O的半徑是
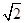 C.2
C.2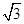 D.
D.