
【題目】如圖,反比例函數![]() 與一次函數y=ax+b的圖象交于點A(2,2)、B(
與一次函數y=ax+b的圖象交于點A(2,2)、B(![]() ,n).
,n).
(1)求這兩個函數解析式;
(2)將一次函數y=ax+b的圖象沿y軸向下平移m個單位,使平移后的圖象與反比例函數![]() 的圖象有且只有一個交點,求m的值.
的圖象有且只有一個交點,求m的值.

【答案】(1)![]() ,y=﹣4x+10;(2)m=2或m=18.
,y=﹣4x+10;(2)m=2或m=18.
【解析】
試題分析:(1)由點A在反比例函數的圖象上,結合反比例函數圖象上的點的坐標特征即可得出反比例函數的解析式;由點B的橫坐標以及反比例函數的解析式即可得出點B的坐標,再由A、B點的坐標利用待定系數法即可求出一次函數得解析式;
(2)結合(1)中得結論找出平移后的直線的解析式,將其代入反比例函數解析式中,整理得出關于x的二次方程,令其根的判別式△=0,即可得出關于m的一元二次方程,解方程即可得出結論.
試題解析:(1)∵A(2,2)在反比例函數![]() 的圖象上,∴k=4,∴反比例函數的解析式為
的圖象上,∴k=4,∴反比例函數的解析式為![]() .
.
又∵點B(![]() ,n)在反比例函數
,n)在反比例函數![]() 的圖象上,∴
的圖象上,∴![]() ,解得:n=8,即點B的坐標為(
,解得:n=8,即點B的坐標為(![]() ,8).
,8).
由A(2,2)、B(![]() ,8)在一次函數y=ax+b的圖象上,得:
,8)在一次函數y=ax+b的圖象上,得: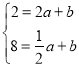 ,解得:
,解得:![]() ,∴一次函數的解析式為y=﹣4x+10.
,∴一次函數的解析式為y=﹣4x+10.
(2)將直線y=﹣4x+10向下平移m個單位得直線的解析式為y=﹣4x+10﹣m,∵直線y=﹣4x+10﹣m與雙曲線![]() 有且只有一個交點,令
有且只有一個交點,令![]() ,得
,得![]() ,∴△=
,∴△=![]() ,解得:m=2或m=18.
,解得:m=2或m=18.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知AB=AC,AE=AF,BE與CF交于點D,則對于下列結論:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分線上.其中正確的是( ) 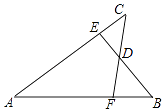
A.①
B.②
C.①和②
D.①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設一次函數y=kx+2k-3(k≠0),對于任意兩個k的值k1,k2,分別對應兩個一次函數值y1,y2,若k1k2<0,當x=m時,取相應y1,y2,中的較小值p,則p的最大值是.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把點(2,﹣3)先向右平移3個單位長度,再向下平移2個單位長度得到的點的坐標是( )
A.(5,﹣1)
B.(﹣1,﹣5)
C.(5,﹣5)
D.(﹣1,﹣1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校隨機抽查了10名參加2016年云南省初中學業水平考試學生的體育成績,得到的結果如表:
成績(分) | 46 | 47 | 48 | 49 | 50 |
人數(人) | 1 | 2 | 1 | 2 | 4 |
下列說法正確的是( )
A.這10名同學的體育成績的眾數為50
B.這10名同學的體育成績的中位數為48
C.這10名同學的體育成績的方差為50
D.這10名同學的體育成績的平均數為48
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是雙曲線y= ![]() 在第一象限上的一動點,連接AO并延長交另一分支于點B,以AB為斜邊作等腰Rt△ABC,點C在第二象限,隨著點A的運動,點C的位置也不斷的變化,但始終在一函數圖象上運動,則這個函數的解析式為( )
在第一象限上的一動點,連接AO并延長交另一分支于點B,以AB為斜邊作等腰Rt△ABC,點C在第二象限,隨著點A的運動,點C的位置也不斷的變化,但始終在一函數圖象上運動,則這個函數的解析式為( ) 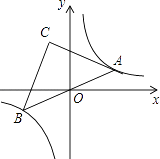
A.y= ![]()
B.y= ![]()
C.y=﹣ ![]()
D.y=﹣ ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com