
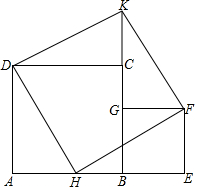
 在線段AE上取一點B使AB>BE,以AB、BE為邊在AE同側作正方形ABCD、BEFG,在AB上取AH=BE在BC的延長線上取K使CK=BE,聯結DK、KF、DH、HF
在線段AE上取一點B使AB>BE,以AB、BE為邊在AE同側作正方形ABCD、BEFG,在AB上取AH=BE在BC的延長線上取K使CK=BE,聯結DK、KF、DH、HF分析 (1)由四邊形ABCD,四邊形BEFG是正方形,得到AD=AB=BC=CD,BE=EF=BG=GF,∠A=∠ABC=∠DCB=∠E=∠BGF=90°,根據全等三角形的性質得到DH=HF=DK=FK,于是得到結論;
(2)設AD=AB=BC=CD=a,BE=EF=BG=GF=b,DH=HF=DK=FK=c,根據圖形的面積得到S正方形ABCD+S正方形BEFG=S正方形HFKD,于是得到結論.
解答 (1)證明:∵四邊形ABCD,四邊形BEFG是正方形,
∴AD=AB=BC=CD,BE=EF=BG=GF,∠A=∠ABC=∠DCB=∠E=∠BGF=90°,
∴∠DCK=∠KGF=90°,
∵AH=BE=CK,
∴AH=EF=GF=CK,BH=CG,
∴HE=GK=CD=AD,
在△ADH與△EHF與△CDK與△GKF中,$\left\{\begin{array}{l}{AD=EH=CD=GK}\\{∠A=∠E=∠DCK=∠FGK}\\{AH=BE=CK=GF}\end{array}\right.$,
∴△ADH≌△EHF≌△CDK≌△GKF,
∴DH=HF=DK=FK,
∴四邊形FHKD為正方形;
(2)解:設AD=AB=BC=CD=a,BE=EF=BG=GF=b,DH=HF=DK=FK=c,
∵S正方形ABCD+S正方形BEFG-S△ADH-S△EFH=S正方形HFKD-S△DCK-S△GFK,
∴S正方形ABCD+S正方形BEFG=S正方形HFKD,
即a2+b2=c2.
點評 本題考查了正方形的性質,勾股定理的字母,全等三角形的判斷和性質,熟練正確正方形的性質是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
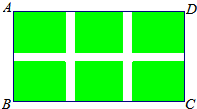 如圖,小區規劃在一個長80m,寬40m的長方形場地上修建三條同樣寬的通道,使其中兩條與DC平行,另一條與BC平行,場地的其余部分種草,通道的寬度為x m.
如圖,小區規劃在一個長80m,寬40m的長方形場地上修建三條同樣寬的通道,使其中兩條與DC平行,另一條與BC平行,場地的其余部分種草,通道的寬度為x m.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
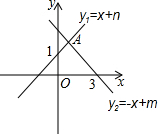 如圖所示,直線y1=x+n與y軸交于點(0,1),直線y2=-x+m與x軸交于點(3,0),兩直線交于點A.不等式x+n≥-x+m的解集為x≥1.
如圖所示,直線y1=x+n與y軸交于點(0,1),直線y2=-x+m與x軸交于點(3,0),兩直線交于點A.不等式x+n≥-x+m的解集為x≥1.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
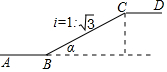 如圖是某商場一樓與二樓之間的手扶電梯示意圖,其中AB、CD分別表示一樓、二樓地面的水平線,電梯坡面BC的坡度i=1:$\sqrt{3}$,則電梯坡面BC的坡角α為( )
如圖是某商場一樓與二樓之間的手扶電梯示意圖,其中AB、CD分別表示一樓、二樓地面的水平線,電梯坡面BC的坡度i=1:$\sqrt{3}$,則電梯坡面BC的坡角α為( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com