
【題目】已知反比例函數(shù)y=![]() 與一次函數(shù)y=kx+b的圖象相交于點A(4,1),B(a,2)兩點,一次函數(shù)的圖象與y軸交于點C,點D在x軸上,其坐標為(1,0),則△ACD的面積為( )
與一次函數(shù)y=kx+b的圖象相交于點A(4,1),B(a,2)兩點,一次函數(shù)的圖象與y軸交于點C,點D在x軸上,其坐標為(1,0),則△ACD的面積為( )
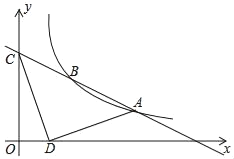
A.12B.9C.6D.5
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4![]() ,點D是AC邊上一動點,連接BD,以AD為直徑的圓交BD于點E,則線段CE長度的最小值為___.
,點D是AC邊上一動點,連接BD,以AD為直徑的圓交BD于點E,則線段CE長度的最小值為___.
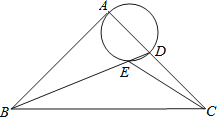
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在半⊙O中,AB是直徑,點D是⊙O上一點,點C是![]() 的中點,CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE,CB于點P,Q,連接AC,關(guān)于下列結(jié)論:①∠BAD=∠ABC;②GP=GD;③點P是△ACQ的外心;④AC2=CQCB,其中結(jié)論正確的是____.
的中點,CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE,CB于點P,Q,連接AC,關(guān)于下列結(jié)論:①∠BAD=∠ABC;②GP=GD;③點P是△ACQ的外心;④AC2=CQCB,其中結(jié)論正確的是____.
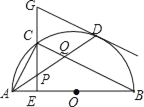
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,反比例函數(shù)y=![]() (k≠0,x>0)的圖象與矩形OABC的邊AB、BC分別交于點E、F,E(
(k≠0,x>0)的圖象與矩形OABC的邊AB、BC分別交于點E、F,E(![]() ,6),且E為BC的中點,D為x軸負半軸上的點.
,6),且E為BC的中點,D為x軸負半軸上的點.

(1)求反比倒函數(shù)的表達式和點F的坐標;
(2)若D(﹣![]() ,0),連接DE、DF、EF,則△DEF的面積是 .
,0),連接DE、DF、EF,則△DEF的面積是 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,D為邊AC上的點,以AD為直徑作⊙O,連接BD并延長交⊙O于點E,連接CE.
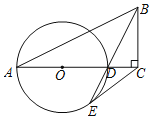
(1)若CE=BC,求證:CE是⊙O的切線.
(2)在(1)的條件下,若CD=2,BC=4,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】方方駕駛小汽車勻速地從A地行使到B地,行駛里程為480千米,設(shè)小汽車的行使時間為t(單位:小時),行使速度為v(單位:千米/小時),且全程速度限定為不超過120千米/小時.
⑴求v關(guān)于t的函數(shù)表達式;
⑵方方上午8點駕駛小汽車從A出發(fā).
①方方需在當天12點48分至14點(含12點48分和14點)間到達B地,求小汽車行駛速度v的范圍.
②方方能否在當天11點30分前到達B地?說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某工廠現(xiàn)有甲種原料360千克,乙種原料290千克,計劃利用這兩種原料生產(chǎn)A、B兩種產(chǎn)品共50件,已知生產(chǎn)一件A種產(chǎn)品用甲種原料9千克,乙種原料3千克,可獲利700元;生產(chǎn)一件B種產(chǎn)品用甲種原料4千克,乙種原料10千克,可獲利1200元.
(1)按要求安排A、B兩種產(chǎn)品的生產(chǎn)件數(shù),有哪幾種方案?請你設(shè)計出來;
(2)設(shè)生產(chǎn)A、B兩種產(chǎn)品總利潤為y元,其中一種產(chǎn)品生產(chǎn)件數(shù)為x件,試寫出y與x之間的函數(shù)關(guān)系式,并利用函數(shù)的性質(zhì)說明那種方案獲利最大?最大利潤是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)y=ax![]() +bx+c的圖象如圖所示,下列結(jié)論:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的實數(shù)),其中正確的結(jié)論有 ( )
+bx+c的圖象如圖所示,下列結(jié)論:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的實數(shù)),其中正確的結(jié)論有 ( )
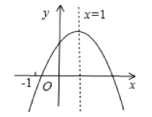
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
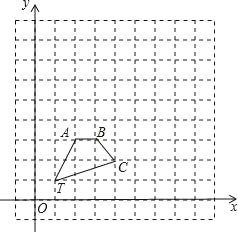
【題目】如圖,在正方形網(wǎng)格中,四邊形TABC的頂點坐標分別為T(1,1),A(2,3),B(3,3),C(4,2).
(1)以點T(1,1)為位似中心,在位似中心的同側(cè)將四邊形TABC放大為原來的2倍,放大后點A,B,C的對應點分別為A′,B′,C′畫出四邊形TA′B′C′;
(2)寫出點A′,B′,C′的坐標:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)為線段AC上任一點,則變化后點D的對應點D′的坐標為 .
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com