題目列表(包括答案和解析)
,故選C. 
答案:C
【命題立意】:本題考查復數的除法運算，分子、分母需要同乘以分母的共軛復數，把分母變為實數，將除法轉變為乘法進行運算.
| 證人所說的顏色（正確率80%） | |||
| 真實顏色 | 綠色（輛） | 紅色（輛） | 合計 |
| 綠色（85%） | 1700 | ||
| 紅色（15%） | 300 | ||
| 合計（輛） | 2000 | ||
如圖，A處建有一個補給站，在A正西120海里處有一個港口B，一艘科考船從B出發，沿北偏東30°的方向，以20海里/小時的速度駛離港口．同時一艘為科考船運送補給的快艇從A出發，沿北偏西30°的方向，以60海里/小時的速度行駛，1小時后補給船行駛至C處，發生故障停留了1小時．快艇為在最短時間內將補給送到科考船，在C處調整航向后繼續以60海里/小時的速度直線行駛，恰好與科考船在D處相遇，求相遇時科考船共行駛了多少小時．命題“若
，
，
，則
．”可以如下證明：構造函數
，則
，因為對一切
，恒有
，所以
，故得．
試解決下列問題：
（1）若，，
，
，求證
；
（2）試將上述命題推廣到n個實數，并證明你的結論．
如圖，四棱錐S—ABCD中，SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E為棱SB上的三等分點，SE=2EB
(Ⅰ)證明：平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .
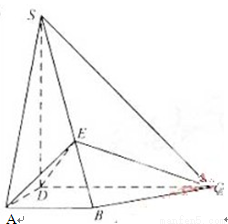
【解析】本試題主要考查了立體幾何中的運用。
(1)證明：因為SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E為棱SB上的三等分點，SE=2EB 所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.，因此可知得到平面EDC⊥平面SBC.
（Ⅱ）由SA2= SD2+AD2 = 5 ，AB=1，SE=2EB，AB⊥SA，知
AE2= (1 /3 SA)2+(2/ 3 AB)2 =1，又AD=1．
故△ADE為等腰三角形．
取ED中點F，連接AF，則AF⊥DE，AF2= AD2-DF2 =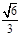
．
連接FG，則FG∥EC，FG⊥DE．
所以，∠AFG是二面角A-DE-C的平面角．
連接AG，AG= 2 ，FG2= DG2-DF2
=
，
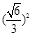cos∠AFG=(AF2+FG2-AG2 )/2⋅AF⋅FG =-1 /2 ，
所以，二面角A-DE-C的大小為120°
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com