
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(2)設函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在正的極值,求實數(shù)
上存在正的極值,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)單調遞減區(qū)間為![]() ,單調遞增區(qū)間為
,單調遞增區(qū)間為![]() ;(2)
;(2)![]()
【解析】
(1)求導后,根據(jù)導函數(shù)的正負可確定所求的單調區(qū)間;
(2)求導后可知![]() 的正負由
的正負由![]() 決定,利用導數(shù)可求得
決定,利用導數(shù)可求得![]() 單調性和最值,根據(jù)
單調性和最值,根據(jù)![]() 在
在![]() 上有極值,可知
上有極值,可知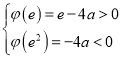 ,解不等式求得
,解不等式求得![]() ;分別在
;分別在![]() 和
和![]() 兩種情況下,根據(jù)
兩種情況下,根據(jù)![]() 單調性確定
單調性確定![]() 上的極值,結合導數(shù)確定極值的正負,從而得到結果.
上的極值,結合導數(shù)確定極值的正負,從而得到結果.
(1)當![]() 時,
時,![]() ,其定義域為
,其定義域為![]() .
.
![]() ,令
,令![]() 得:
得:![]() ,令
,令![]() 得:
得:![]() ,
,
![]() 的單調遞減區(qū)間為
的單調遞減區(qū)間為![]() ,單調遞增區(qū)間為
,單調遞增區(qū)間為![]() .
.
(2)![]() ,
,
![]() ,
,
令![]() ,
,![]() ,則
,則![]() .
.
令![]() 得:
得:![]() ,令
,令![]() 得:
得:![]() ,
,![]() 函數(shù)
函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調遞增,在區(qū)間
上單調遞增,在區(qū)間![]() 上單調遞減,
上單調遞減,
又![]() ,
,![]() ,
,![]() ,顯然
,顯然![]() .
.
若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在極值,則
上存在極值,則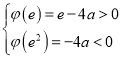 ,解得:
,解得:![]() .
.
①當 ,即
,即![]() 時,一定存在
時,一定存在![]() ,使得
,使得![]() ,
,
不妨設![]() ,則此時
,則此時![]() ,
,![]() 在區(qū)間
在區(qū)間![]() 上為負,在區(qū)間
上為負,在區(qū)間![]() 上為正,在區(qū)間
上為正,在區(qū)間![]() 上為負,
上為負,
![]() 在區(qū)間
在區(qū)間![]() 上為負,在區(qū)間
上為負,在區(qū)間![]() 上為正,在區(qū)間
上為正,在區(qū)間![]() 上為負,
上為負,
![]() 在區(qū)間
在區(qū)間![]() 上單調遞減,在區(qū)間
上單調遞減,在區(qū)間![]() 上單調遞增,在區(qū)間
上單調遞增,在區(qū)間![]() 上單調遞減,
上單調遞減,
![]() ,
,![]() .
.
![]() 當
當![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在兩個極值
上存在兩個極值![]() ,
,![]() ,且
,且![]() .
.
![]() ,令
,令![]() ,其中
,其中![]() .
.
![]() ,
,![]() 在區(qū)間
在區(qū)間![]() 上單調遞增,
上單調遞增,
即當![]() 時,
時,![]() ,
,![]() ,
,
![]() 當
當![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的極值滿足
上的極值滿足![]() ,即函數(shù)
,即函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在正的極值.
上存在正的極值.
②當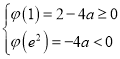 ,即
,即![]() 時,一定存在
時,一定存在![]() ,使得
,使得![]() ,使得函數(shù)
,使得函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調遞增,在區(qū)間
上單調遞增,在區(qū)間![]() 上單調遞減.
上單調遞減.
則函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的極大值是
上的極大值是![]() ,且
,且![]() ,
,
![]() 當
當![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上存在正的極值.
上存在正的極值.
綜上所述:當![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在正的極值.
上存在正的極值.


 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() :
:![]() ,直線
,直線![]() :
:![]() .
.![]() 為圓
為圓![]() 內一點,弦
內一點,弦![]() 過點
過點![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() .
.
(1)若![]() ,求
,求![]() 的面積;
的面積;
(2)判斷直線![]() 與圓
與圓![]() 的位置關系,并證明.
的位置關系,并證明.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() .點E為橢圓在第一象限內一點,點F在橢圓上且與點E關于原點對稱,直線
.點E為橢圓在第一象限內一點,點F在橢圓上且與點E關于原點對稱,直線![]() 與橢圓交于A,B兩點,則點E,F到直線x+y-1=0的距離之和的最大值是________;此時四邊形AEBF的面積是________.
與橢圓交于A,B兩點,則點E,F到直線x+y-1=0的距離之和的最大值是________;此時四邊形AEBF的面積是________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() 的焦點到直線
的焦點到直線![]() 的距離為
的距離為![]() ,過點
,過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
(1)求拋物線![]() 的準線方程;
的準線方程;
(2)設直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,若
,若![]() ,且
,且![]() 與
與![]() 的交點在拋物線
的交點在拋物線![]() 上,求直線
上,求直線![]() 的斜率和點
的斜率和點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,其中e是自然對數(shù)的底數(shù).
,其中e是自然對數(shù)的底數(shù).
(1)若函數(shù)![]() 的極大值為
的極大值為![]() ,求實數(shù)a的值;
,求實數(shù)a的值;
(2)當a=e時,若曲線![]() 與
與![]() 在
在![]() 處的切線互相垂直,求
處的切線互相垂直,求![]() 的值;
的值;
(3)設函數(shù)![]() ,若
,若![]() >0對任意的x
>0對任意的x![]() (0,1)恒成立,求實數(shù)a的取值范圍.
(0,1)恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】過正四面體ABCD的頂點A作一個形狀為等腰三角形的截面,且使截面與底面BCD所成的角為![]() ,這樣的截面有( )
,這樣的截面有( )
A.6個B.12個C.16個D.18個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() ,
,![]() 、
、![]() 分別是其左、右焦點,過
分別是其左、右焦點,過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且橢圓
兩點,且橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 的周長等于
的周長等于![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)當![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著網上購物的普及,傳統(tǒng)的實體店遭受到了強烈的沖擊,某商場實體店近九年來的純利潤如下表所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
時間代號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
實體店純利潤 | 2 | 2.3 | 2.5 | 2.9 | 3 | 2.5 | 2.1 | 1.7 | 1.2 |
根據(jù)這9年的數(shù)據(jù),對![]() 和
和![]() 作線性相關性檢驗,求得樣本相關系數(shù)的絕對值為0.254;根據(jù)后5年的數(shù)據(jù),對
作線性相關性檢驗,求得樣本相關系數(shù)的絕對值為0.254;根據(jù)后5年的數(shù)據(jù),對![]() 和
和![]() 作線性相關性檢驗,求得樣本相關系數(shù)的絕對值為0.985;
作線性相關性檢驗,求得樣本相關系數(shù)的絕對值為0.985;
(1)如果要用線性回歸方程預測該商場2019年實體店純利潤,現(xiàn)有兩個方案:
方案一:選取這9年的數(shù)據(jù),進行預測;
方案二:選取后5年的數(shù)據(jù)進行預測.
從生活實際背景以及相關性檢驗的角度分析,你覺得哪個方案更合適.
附:相關性檢驗的臨界值表:
| 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
7 | 0.666 | 0.798 |
(2)某機構調研了大量已經開店的店主,據(jù)統(tǒng)計,只開網店的占調查總人數(shù)的![]() ,既開網店又開實體店的占調查總人數(shù)的
,既開網店又開實體店的占調查總人數(shù)的![]() ,現(xiàn)以此調查統(tǒng)計結果作為概率,若從上述統(tǒng)計的店主中隨機抽查了5位,求只開實體店的人數(shù)的分布列及期望.
,現(xiàn)以此調查統(tǒng)計結果作為概率,若從上述統(tǒng)計的店主中隨機抽查了5位,求只開實體店的人數(shù)的分布列及期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】國家正積極推行垃圾分類工作,教育部辦公廳等六部門也發(fā)布了《關于在學校推進生活垃圾分類管理工作的通知》.《通知》指出,到2020年底,各學校生活垃圾分類知識普及率要達到100%某市教育主管部門據(jù)此做了“哪些活動最能促進學生進行垃圾分類”的問卷調查(每個受訪者只能在問卷的4個活動中選擇一個)如圖是調查結果的統(tǒng)計圖,以下結論正確的是( )
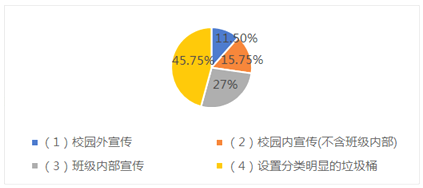
A.回答該問卷的受訪者中,選擇的(2)和(3)人數(shù)總和比選擇(4)的人數(shù)多
B.回該問卷的受訪者中,選擇“校園外宣傳”的人數(shù)不是最少的
C.回答該問卷的受訪者中,選擇(4)的人數(shù)比選擇(2)的人數(shù)可能多30人
D.回答該問卷的總人數(shù)不可能是1000人
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com