
【題目】已知函數(shù)![]() .
.
(Ⅰ)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(Ⅱ)求證:當(dāng)![]() 時(shí),
時(shí),![]() ;
;
(Ⅲ)設(shè)實(shí)數(shù)k使得![]() 對(duì)
對(duì)![]() 恒成立,求k的最大值.
恒成立,求k的最大值.
【答案】(Ⅰ)![]() ,(Ⅱ)證明見(jiàn)解析,(Ⅲ)k的最大值為2.
,(Ⅱ)證明見(jiàn)解析,(Ⅲ)k的最大值為2.
【解析】
(Ⅰ)![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,曲線y=f(x)在點(diǎn)(0,f(0))處的切線方程為
,曲線y=f(x)在點(diǎn)(0,f(0))處的切線方程為![]()
(Ⅱ)當(dāng)![]() 時(shí),
時(shí),![]() ,即不等式
,即不等式![]() ,對(duì)
,對(duì)![]() 成立,設(shè)
成立,設(shè)![]() ,則
,則![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,故
,故![]() 在(0,1)上為增函數(shù),則
在(0,1)上為增函數(shù),則![]() ,因此對(duì)
,因此對(duì)![]() ,
,![]() 成立;
成立;
(Ⅲ)使![]() 成立,
成立,![]() ,等價(jià)于
,等價(jià)于![]() ,
,![]() ;
;![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,函數(shù)在(0,1)上為增函數(shù),
,函數(shù)在(0,1)上為增函數(shù),![]() ,符合題意;
,符合題意;
當(dāng)![]() 時(shí),令
時(shí),令![]() ,
,![]() ,不合題意,
,不合題意,
所以k的最大值為2.
【考點(diǎn)精析】掌握導(dǎo)數(shù)的幾何意義是解答本題的根本,需要知道通過(guò)圖像,我們可以看出當(dāng)點(diǎn)![]() 趨近于
趨近于![]() 時(shí),直線
時(shí),直線![]() 與曲線相切.容易知道,割線
與曲線相切.容易知道,割線![]() 的斜率是
的斜率是![]() ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)![]() 趨近于
趨近于![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 在
在![]() 處的導(dǎo)數(shù)就是切線PT的斜率k,即
處的導(dǎo)數(shù)就是切線PT的斜率k,即![]() .
.


 探究與鞏固河南科學(xué)技術(shù)出版社系列答案
探究與鞏固河南科學(xué)技術(shù)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某同學(xué)用“五點(diǎn)法”畫函數(shù)![]() 在某一個(gè)周期內(nèi)的圖象時(shí),列表并填入了部分?jǐn)?shù)據(jù),如下表:
在某一個(gè)周期內(nèi)的圖象時(shí),列表并填入了部分?jǐn)?shù)據(jù),如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 5 | -5 | 0 |
(Ⅰ)請(qǐng)將上表數(shù)據(jù)補(bǔ)充完整,填寫在答題卡上相應(yīng)位置,并直接寫出函數(shù)![]() 的解析式;
的解析式;
(Ⅱ)將![]() 圖象上所有點(diǎn)向左平行移動(dòng)
圖象上所有點(diǎn)向左平行移動(dòng)![]() 個(gè)單位長(zhǎng)度,得到
個(gè)單位長(zhǎng)度,得到![]() 的圖象. 若
的圖象. 若![]() 圖象的一個(gè)對(duì)稱中心為
圖象的一個(gè)對(duì)稱中心為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著我國(guó)經(jīng)濟(jì)的發(fā)展,居民的儲(chǔ)蓄存款逐年增長(zhǎng).設(shè)某地區(qū)城鄉(xiāng)居民人民幣儲(chǔ)蓄存款(年底余額)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
時(shí)間代號(hào)t | 1 | 2 | 3 | 4 | 5 |
儲(chǔ)蓄存款y(千億元) | 5 | 6 | 7 | 8 | 10 |
(1)求y關(guān)于t的回歸方程![]()
(2)用所求回歸方程預(yù)測(cè)該地區(qū)2015年(![]() )的人民幣儲(chǔ)蓄存款.
)的人民幣儲(chǔ)蓄存款.
附:回歸方程![]() 中
中
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·陜西)△ABC的內(nèi)角A,B,C所對(duì)的邊分別為a,b,c.向量![]() 與
與![]() 平行.
平行.
(1)求A。
(2)若a=![]() , b=2求△ABC的面積。
, b=2求△ABC的面積。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·陜西)在直角坐標(biāo)系xOy中,直線l的參數(shù)方程為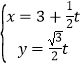 (t為參數(shù)).以原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,
(t為參數(shù)).以原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,![]() c的極坐標(biāo)方程為
c的極坐標(biāo)方程為![]() =2
=2![]() sin
sin![]() .
.
(1)寫出![]() c的直角坐標(biāo)方程;
c的直角坐標(biāo)方程;
(2)P為直線l上一動(dòng)點(diǎn),當(dāng)P到圓心C的距離最小時(shí),求P的直角坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若將函數(shù)y=2sin 2x的圖像向左平移 ![]() 個(gè)單位長(zhǎng)度,則評(píng)議后圖象的對(duì)稱軸為( )
個(gè)單位長(zhǎng)度,則評(píng)議后圖象的對(duì)稱軸為( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已成橢圓 ![]() 的左右頂點(diǎn)分別為
的左右頂點(diǎn)分別為 ![]() ,上下頂點(diǎn)分別為
,上下頂點(diǎn)分別為 ![]() ,左右焦點(diǎn)分別為
,左右焦點(diǎn)分別為 ![]() ,其中長(zhǎng)軸長(zhǎng)為4,且圓
,其中長(zhǎng)軸長(zhǎng)為4,且圓 ![]() 為菱形
為菱形 ![]() 的內(nèi)切圓.
的內(nèi)切圓.
(1)求橢圓 ![]() 的方程;
的方程;
(2)點(diǎn) ![]() 為
為 ![]() 軸正半軸上一點(diǎn),過(guò)點(diǎn)
軸正半軸上一點(diǎn),過(guò)點(diǎn) ![]() 作橢圓
作橢圓 ![]() 的切線
的切線 ![]() ,記右焦點(diǎn)
,記右焦點(diǎn) ![]() 在
在 ![]() 上的射影為
上的射影為 ![]() ,若
,若 ![]() 的面積不小于
的面積不小于 ![]() ,求
,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知兩個(gè)集合A,B,滿足BA.若對(duì)任意的x∈A,存在ai , aj∈B(i≠j),使得x=λ1ai+λ2aj(λ1 , λ2∈{﹣1,0,1}),則稱B為A的一個(gè)基集.若A={1,2,3,4,5,6,7,8,9,10},則其基集B元素個(gè)數(shù)的最小值是 .
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com