
已知二次函數(shù) 的導函數(shù)的圖像與直線
的導函數(shù)的圖像與直線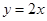 平行,且
平行,且 在
在 處取得極小值
處取得極小值 .設
.設 .
.
(1)若曲線 上的點
上的點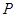 到點
到點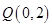 的距離的最小值為
的距離的最小值為 ,求
,求 的值;
的值;
(2)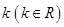 如何取值時,函數(shù)
如何取值時,函數(shù) 存在零點,并求出零點.
存在零點,并求出零點.
(1) 或
或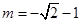 ;(2)詳見解析.
;(2)詳見解析.
解析試題分析:(1)先設點 的坐標,利用兩點間的距離公式將
的坐標,利用兩點間的距離公式將 表示為
表示為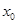 為自變量的函數(shù),利用基本不等式求出相應的最小值,然后列方程求出
為自變量的函數(shù),利用基本不等式求出相應的最小值,然后列方程求出 的值;(2)令
的值;(2)令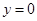 ,將函數(shù)
,將函數(shù) 的零點轉化為求方程
的零點轉化為求方程 的根,對首項系數(shù)
的根,對首項系數(shù) 的符號進行分類討論,以及在首項系數(shù)不為零時對
的符號進行分類討論,以及在首項系數(shù)不為零時對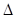 的符號進行分類討論,從而確定函數(shù)在定義域上是否存在零點,并且在零點存在的前提下利用求根公式求出相應的零點值.
的符號進行分類討論,從而確定函數(shù)在定義域上是否存在零點,并且在零點存在的前提下利用求根公式求出相應的零點值.
試題解析:(1)依題可設 (
(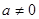 ),則
),則 ;
;
又 的圖像與直線
的圖像與直線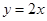 平行
平行 
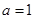
 ,
,  ,
,
設 ,則
,則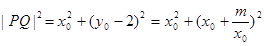

當且僅當 時,
時, 取得最小值,即
取得最小值,即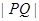 取得最小值
取得最小值
當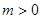 時,
時,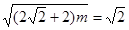 解得
解得
當 時,
時,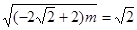 解得
解得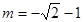
(2)由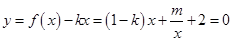 (
(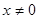 ),得
),得

當 時,方程
時,方程 有一解
有一解 ,函數(shù)
,函數(shù) 有一零點
有一零點 ;
;
當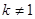 時,方程
時,方程 有二解
有二解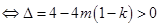 ,
,
若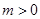 ,
, ,
,
函數(shù) 有兩個零點
有兩個零點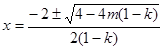 ,即
,即 ;
;
若 ,
, ,
,
函數(shù) 有兩個零點
有兩個零點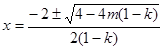 ,即
,即 ;
;
當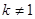 時,方程
時,方程 有一解
有一解 ,
,  ,
,
函數(shù) 有一零點
有一零點
綜上,當 時, 函數(shù)
時, 函數(shù) 有一零點
有一零點 ;
;
當 (
(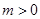 ),或
),或 (
( )時,
)時,
函數(shù) 有兩個零點
有兩個零點 ;
;
當 時,函數(shù)
時,函數(shù) 有一零點
有一零點 .
.
考點:1.兩點間的距離公式;2.基本不等式;3.分類討論;4.一元二次方程的求解


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數(shù)學 來源: 題型:解答題
我國加入WTO后,根據(jù)達成的協(xié)議,若干年內(nèi)某產(chǎn)品關稅與市場供應量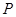 的關系允許近似的滿足:
的關系允許近似的滿足: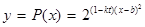 (其中
(其中 為關稅的稅率,且
為關稅的稅率,且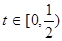 ,
, 為市場價格,
為市場價格,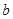 、
、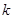 為正常數(shù)),當
為正常數(shù)),當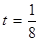 時的市場供應量曲線如圖:
時的市場供應量曲線如圖: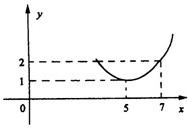
(1)根據(jù)圖象求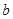 、
、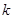 的值;
的值;
(2)若市場需求量為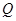 ,它近似滿足
,它近似滿足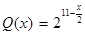 .當
.當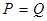 時的市場價格稱為市場平衡價格.為使市場平衡價格控制在不低于9元,求稅率
時的市場價格稱為市場平衡價格.為使市場平衡價格控制在不低于9元,求稅率 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某自來水廠的蓄水池存有400噸水,水廠每小時可向蓄水池中注水60噸,同時蓄水池又向居民小區(qū)不間斷供水,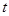 小時內(nèi)供水總量為
小時內(nèi)供水總量為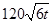 噸(
噸(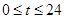 ),從供水開始到第幾小時時,蓄水池中的存水量最少?最少水量是多少噸?
),從供水開始到第幾小時時,蓄水池中的存水量最少?最少水量是多少噸?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設 ,兩個函數(shù)
,兩個函數(shù) ,
, 的圖像關于直線
的圖像關于直線 對稱.
對稱.
(1)求實數(shù) 滿足的關系式;
滿足的關系式;
(2)當 取何值時,函數(shù)
取何值時,函數(shù) 有且只有一個零點;
有且只有一個零點;
(3)當 時,在
時,在 上解不等式
上解不等式 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知偶函數(shù)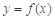 滿足:當
滿足:當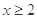 時,
時,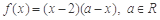 ,當
,當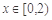 時,
時,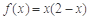 .
.
(1)求當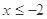 時,
時,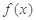 的表達式;
的表達式;
(2)試討論:當實數(shù)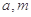 滿足什么條件時,函數(shù)
滿足什么條件時,函數(shù)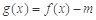 有4個零點,且這4個零點從小到大依次構成等差數(shù)列.
有4個零點,且這4個零點從小到大依次構成等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
在不考慮空氣阻力的情況下,火箭的最大速度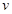 (單位:
(單位: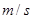 )和燃料的質(zhì)量
)和燃料的質(zhì)量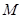 (單位:
(單位: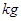 ),火箭(除燃料外)的質(zhì)量
),火箭(除燃料外)的質(zhì)量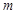 (單位:
(單位: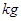 )滿足
)滿足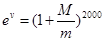 .(
.(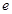 為自然對數(shù)的底)
為自然對數(shù)的底)
(Ⅰ)當燃料質(zhì)量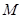 為火箭(除燃料外)質(zhì)量
為火箭(除燃料外)質(zhì)量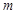 兩倍時,求火箭的最大速度(單位:
兩倍時,求火箭的最大速度(單位: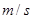 );
);
(Ⅱ)當燃料質(zhì)量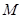 為火箭(除燃料外)質(zhì)量
為火箭(除燃料外)質(zhì)量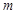 多少倍時,火箭的最大速度可以達到8
多少倍時,火箭的最大速度可以達到8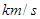 .(結果精確到個位,數(shù)據(jù):
.(結果精確到個位,數(shù)據(jù):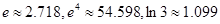 )
)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com