
【題目】在疫情這一特殊時期,教育行政部門部署了“停課不停學”的行動,全力幫助學生在線學習.復課后進行了摸底考試,某校數(shù)學教師為了調(diào)查高三學生這次摸底考試的數(shù)學成績與在線學習數(shù)學時長之間的相關關系,對在校高三學生隨機抽取45名進行調(diào)查.知道其中有25人每天在線學習數(shù)學的時長是不超過1小時的,得到了如下的等高條形圖:
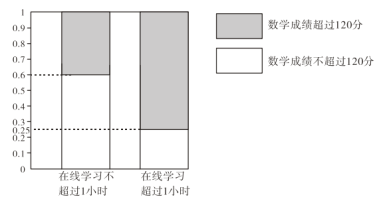
(Ⅰ)是否有![]() 的把握認為“高三學生的這次摸底考試數(shù)學成績與其在線學習時長有關”;
的把握認為“高三學生的這次摸底考試數(shù)學成績與其在線學習時長有關”;
(Ⅱ)將頻率視為概率,從全校高三學生這次數(shù)學成績超過120分的學生中隨機抽取10人,求抽取的10人中每天在線學習時長超過1小時的人數(shù)的數(shù)學期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
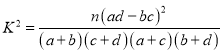
【答案】(Ⅰ)沒有;(Ⅱ)![]() ,
,![]() .
.
【解析】
(1)根據(jù)條形圖提供的數(shù)據(jù)完成列聯(lián)表,然后再將數(shù)據(jù)代入公式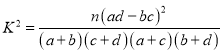 ,求得
,求得![]() ,與臨界表對比下結(jié)論.
,與臨界表對比下結(jié)論.
(2)由列聯(lián)表得到數(shù)學成績超過120分的學生每天在線學習時長超過1小時的概率,然后用二項分布的期望和方差公式求解.
(Ⅰ)依題意,得![]() 列聯(lián)表
列聯(lián)表
在線學習時長 |
|
| 合計 |
| 15 | 10 | 25 |
| 5 | 15 | 20 |
合計 | 20 | 25 | 45 |
∵![]()
∴沒有![]() 的把握認為“高三學生的這次摸底成績與其在線學習時長有關”;
的把握認為“高三學生的這次摸底成績與其在線學習時長有關”;
(Ⅱ)從上述![]() 列聯(lián)表中可以看出:
列聯(lián)表中可以看出:
這次數(shù)學成績超過120分的學生中每天在線學習時長超過1小時的頻率為![]() ,
,
則![]() ,
,
∴![]() ,
,![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】![]() 市某機構為了調(diào)查該市市民對我國申辦
市某機構為了調(diào)查該市市民對我國申辦![]() 年足球世界杯的態(tài)度,隨機選取了
年足球世界杯的態(tài)度,隨機選取了![]() 位市民進行調(diào)查,調(diào)查結(jié)果統(tǒng)計如下:
位市民進行調(diào)查,調(diào)查結(jié)果統(tǒng)計如下:
支持 | 不支持 | 合計 | |
男性市民 |
| ||
女性市民 |
| ||
合計 |
|
|
(1)根據(jù)已知數(shù)據(jù),把表格數(shù)據(jù)填寫完整;
(2)利用(1)完成的表格數(shù)據(jù)回答下列問題:
(i)能否在犯錯誤的概率不超過![]() 的前提下認為支持申辦足球世界杯與性別有關;
的前提下認為支持申辦足球世界杯與性別有關;
(ii)已知在被調(diào)查的支持申辦足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教師,現(xiàn)從這
位是教師,現(xiàn)從這![]() 位退休老人中隨機抽取
位退休老人中隨機抽取![]() 人,求至多有
人,求至多有![]() 位老師的概率.
位老師的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】《山東省高考改革試點方案》規(guī)定:從2017年秋季高中入學的新生開始,不分文理科;2020年高考總成績由語數(shù)外三門統(tǒng)考科目和物理、化學等六門選考科目組成,將每門選考科目的考生原始成績從高到低劃分為![]() 、
、![]() 、
、![]() 、
、![]() 共8個等級,參照正態(tài)分布原則,確定各等級人數(shù)所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%,選考科目成績計入考生總成績時,將A至E等級內(nèi)的考生原始成績,依照等比例轉(zhuǎn)換法則,分別轉(zhuǎn)換到
共8個等級,參照正態(tài)分布原則,確定各等級人數(shù)所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%,選考科目成績計入考生總成績時,將A至E等級內(nèi)的考生原始成績,依照等比例轉(zhuǎn)換法則,分別轉(zhuǎn)換到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 八個分數(shù)區(qū)間,得到考生的等級成績.某市高一學生共6000人,為給高一學生合理選科提供依據(jù),對六門選考科目進行測試,其中化學考試原始成績
八個分數(shù)區(qū)間,得到考生的等級成績.某市高一學生共6000人,為給高一學生合理選科提供依據(jù),對六門選考科目進行測試,其中化學考試原始成績![]() 大致服從正態(tài)分布
大致服從正態(tài)分布![]() .
.
(1)求該市化學原始成績在區(qū)間![]() 的人數(shù);
的人數(shù);
(2)以各等級人數(shù)所占比例作為各分數(shù)區(qū)間發(fā)生的概率,按高考改革方案,若從全省考生中隨機抽取3人,記X表示這3人中等級成績在區(qū)間![]() 的人數(shù),求
的人數(shù),求![]() .
.
(附:若隨機變量![]() ,則
,則![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
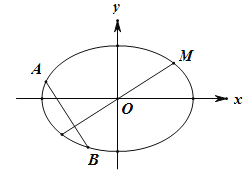
【題目】如圖,橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() .已知點
.已知點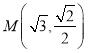 在橢圓上,且點M到兩焦點距離之和為4.
在橢圓上,且點M到兩焦點距離之和為4.
(1)求橢圓的方程;
(2)設與MO(O為坐標原點)垂直的直線交橢圓于A,B(A,B不重合),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了適應高考改革,某中學推行“創(chuàng)新課堂”教學.高一平行甲班采用“傳統(tǒng)教學”的教學方式授課,高一平行乙班采用“創(chuàng)新課堂”的教學方式授課,為了比較教學效果,期中考試后,分別從兩個班中各隨機抽取![]() 名學生的成績進行統(tǒng)計分析,結(jié)果如下表:(記成績不低于
名學生的成績進行統(tǒng)計分析,結(jié)果如下表:(記成績不低于![]() 分者為“成績優(yōu)秀”)
分者為“成績優(yōu)秀”)
分數(shù) |
|
|
|
|
|
|
|
甲班頻數(shù) |
|
|
|
|
|
|
|
乙班頻數(shù) |
|
|
|
|
|
|
|
(Ⅰ)由以上統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 以上的把握認為“成績優(yōu)秀與教學方式有關”?
以上的把握認為“成績優(yōu)秀與教學方式有關”?
甲班 | 乙班 | 總計 | |
成績優(yōu)秀 | |||
成績不優(yōu)秀 | |||
總計 |
(Ⅱ)現(xiàn)從上述樣本“成績不優(yōu)秀”的學生中,抽取![]() 人進行考核,記“成績不優(yōu)秀”的乙班人數(shù)為
人進行考核,記“成績不優(yōu)秀”的乙班人數(shù)為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
參考公式:![]() ,其中
,其中![]() .
.
臨界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列有關說法正確的是( )
A.![]() 的展開式中含
的展開式中含![]() 項的二項式系數(shù)為20;
項的二項式系數(shù)為20;
B.事件![]() 為必然事件,則事件
為必然事件,則事件![]() 、
、![]() 是互為對立事件;
是互為對立事件;
C.設隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,若
,若![]() ,則
,則![]() 與
與![]() 的值分別為
的值分別為![]() ,
,![]() ;
;
D.甲、乙、丙、丁4個人到4個景點旅游,每人只去一個景點,設事件![]() “4個人去的景點各不相同”,事件
“4個人去的景點各不相同”,事件![]() “甲獨自去一個景點”,則
“甲獨自去一個景點”,則![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,底面四邊形
,底面四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點.
上一點.

(1)若![]() ,則在線段
,則在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,請確定
?若存在,請確定![]() 點的位置;若不存在,請說明理由
點的位置;若不存在,請說明理由
(2)己知![]() ,若異面直線
,若異面直線![]() 與
與![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值為
的余弦值為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列判斷正確的是( )
A.線性回歸直線![]() 必經(jīng)過點
必經(jīng)過點![]() ,
,![]() ,…
,…![]() 中心點
中心點![]()
B.從獨立性檢驗可知有99%的把握認為吃地溝油與患胃腸癌有關系時,我們就說如果某人吃地溝油,那么他有99%可能患胃腸癌
C.若兩個隨機變量的線性相關性越強,則相關系數(shù)![]() 的絕對值越接近于1
的絕對值越接近于1
D.將一組數(shù)據(jù)的每一個數(shù)據(jù)都加上或減去同一個常數(shù)后,其方差也要加上或減去這個常數(shù)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com