
已知函數(shù)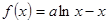 .
.
(1)當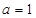 時,求
時,求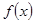 的極值;
的極值;
(2)若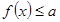 對
對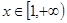 恒成立,求實數(shù)
恒成立,求實數(shù)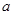 的取值范圍.
的取值范圍.
(1)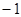 (2)
(2) 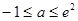
解析試題分析:
(1)確定定義域,保證函數(shù)有意義;求導函數(shù),令其等于0,得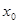 ,判斷其單調性,從而確定其極值.
,判斷其單調性,從而確定其極值.
(2)根據(jù)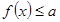 對
對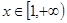 恒成立,可知函數(shù)
恒成立,可知函數(shù)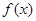 在
在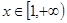 上的最大值小于等于
上的最大值小于等于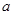 恒成立.利用導數(shù), 通過討論
恒成立.利用導數(shù), 通過討論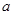 的范圍,判斷函數(shù)的單調性,從而找到函數(shù)的最值,最終確定
的范圍,判斷函數(shù)的單調性,從而找到函數(shù)的最值,最終確定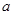 的范圍.
的范圍.
(1)函數(shù)的定義域為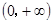 ,由
,由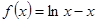 ,知
,知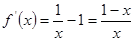 .
.
令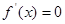 ,得
,得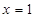 .顯然
.顯然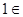
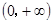 .
.
當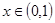 時,
時,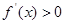
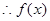 是增函數(shù);
是增函數(shù);
當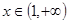 時,
時,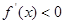
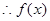 是減函數(shù).
是減函數(shù).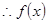 的極大值
的極大值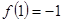 .
.
(2)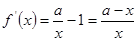 ,
,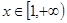
①當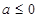 時,
時,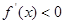
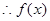 是減函數(shù),即
是減函數(shù),即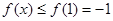
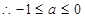 ;
;
②當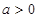 時,當
時,當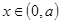 時,
時,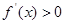
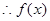 是增函數(shù);
是增函數(shù);
當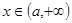 時,
時,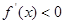
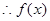 是減函數(shù).
是減函數(shù).
(ⅰ)當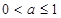 時, 在
時, 在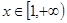 時
時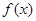 是減函數(shù),即
是減函數(shù),即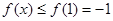
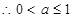 ;
;
(ⅱ) 當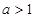 時,當
時,當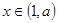 時,
時,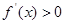
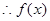 是增函數(shù);當
是增函數(shù);當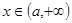 時,
時,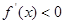
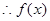 是減函數(shù).
是減函數(shù).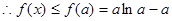 即
即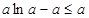
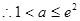 .綜上
.綜上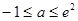 .
.
考點:導數(shù)法求極值,分類討論最值.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)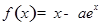
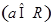 ,
,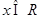 .已知函數(shù)
.已知函數(shù)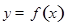 有兩個零點
有兩個零點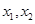 ,且
,且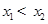 .
.
(1)求 的取值范圍;
的取值范圍;
(2)證明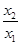 隨著
隨著 的減小而增大;
的減小而增大;
(3)證明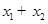 隨著
隨著 的減小而增大.
的減小而增大.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)f(x)=sinx,g(x)=mx-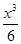 (m為實數(shù)).
(m為實數(shù)).
(1)求曲線y=f(x)在點P(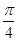 ),f(
),f(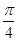 )處的切線方程;
)處的切線方程;
(2)求函數(shù)g(x)的單調遞減區(qū)間;
(3)若m=1,證明:當x>0時,f(x)<g(x)+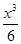 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知曲線 y = x3 + x-2 在點 P0 處的切線  平行直線
平行直線
4x-y-1=0,且點 P0 在第三象限,
求P0的坐標; ⑵若直線 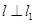 , 且 l 也過切點P0 ,求直線l的方程.
, 且 l 也過切點P0 ,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
用長為18 m的鋼條圍成一個長方體容器的框架,如果所制的容器的長與寬之比為2∶1,那么高為多少時容器的容積最大?并求出它的最大容積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)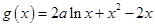 .
.
(1)當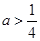 時,討論函數(shù)
時,討論函數(shù)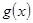 的單調性;
的單調性;
(2)當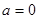 時,在函數(shù)
時,在函數(shù)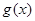 圖象上取不同兩點A、B,設線段AB的中點為
圖象上取不同兩點A、B,設線段AB的中點為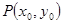 ,試探究函數(shù)
,試探究函數(shù)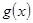 在Q
在Q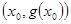 點處的切線與直線AB的位置關系?
點處的切線與直線AB的位置關系?
(3)試判斷當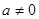 時
時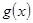 圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)f(x)=x3-ax2-3x.
(1)若f(x)在[1,+∞)上是增函數(shù),求實數(shù)a的取值范圍;
(2)若x=3是f(x)的極值點,求f(x)的單調區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(14分)(2011•福建)已知a,b為常數(shù),且a≠0,函數(shù)f(x)=﹣ax+b+axlnx,f(e)=2(e=2.71828…是自然對數(shù)的底數(shù)).
(I)求實數(shù)b的值;
(II)求函數(shù)f(x)的單調區(qū)間;
(III)當a=1時,是否同時存在實數(shù)m和M(m<M),使得對每一個t∈[m,M],直線y=t與曲線y=f(x)(x∈[ ,e])都有公共點?若存在,求出最小的實數(shù)m和最大的實數(shù)M;若不存在,說明理由.
,e])都有公共點?若存在,求出最小的實數(shù)m和最大的實數(shù)M;若不存在,說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com