
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,點
,點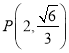 在橢圓上.
在橢圓上.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() ,交橢圓
,交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,坐標原點
上,坐標原點![]() 恰為
恰為![]() 的重心,求直線
的重心,求直線![]() 的方程.
的方程.
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為正方形,PD⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.

(I)證明:平面PQC⊥平面DCQ
(II)求二面角Q-BP-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() ,若
,若![]() (
(![]() 是與
是與![]() 無關的常數,
無關的常數,![]() )則稱數列
)則稱數列![]() 叫做“弱等差數列”已知數列
叫做“弱等差數列”已知數列![]() 滿足:
滿足:![]() 且
且![]() ,對于
,對于![]() 恒成立,(其中
恒成立,(其中![]() 都是常數)
都是常數)
(1)求證:數列![]() 是“弱等差數列”,并求出數列
是“弱等差數列”,并求出數列![]() 的通項公式
的通項公式
(2)當![]() 時,若數列
時,若數列![]() 是單調遞增數列,求
是單調遞增數列,求![]() 的取值范圍
的取值范圍
(3)若![]() ,且
,且![]() ,數列
,數列![]() 滿足:
滿足:![]() ,求
,求![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() ),都在函數
),都在函數![]() (
(![]() ,
,![]() )的圖像上;
)的圖像上;
(1)若數列![]() 是等差數列,求證:數列
是等差數列,求證:數列![]() 是等比數列;
是等比數列;
(2)設![]() ,函數
,函數![]() 的反函數為
的反函數為![]() ,若函數
,若函數![]() 與函數
與函數![]() 的圖像有公共點
的圖像有公共點![]() ,求證:
,求證:![]() 在直線
在直線![]() 上;
上;
(3)設![]() ,
,![]() (
(![]() ),過點
),過點![]() 、
、![]() 的直線
的直線![]() 與兩坐標軸圍成的三角形面積為
與兩坐標軸圍成的三角形面積為![]() ,問:數列
,問:數列![]() 是否存在最大項?若存在,求出最大項的值,若不存在,請說明理由;
是否存在最大項?若存在,求出最大項的值,若不存在,請說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 、
、![]() 與平面
與平面![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,
,![]() ,則下列命題中正確的是( )
,則下列命題中正確的是( )
A.![]() 是
是![]() 的充分不必要條件
的充分不必要條件
B.![]() 是
是![]() 的充要條件
的充要條件
C.設![]() ,則
,則![]() 是
是![]() 的必要不充分條件
的必要不充分條件
D.設![]() ,則
,則![]() 是
是![]() 的既不充分也不必要條件
的既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司舉辦捐步公益活動,參與者通過捐贈每天的運動步數獲得公司提供的牛奶,再將牛奶捐贈給留守兒童.此活動不但為公益事業作出了較大的貢獻,公司還獲得了相應的廣告效益.據測算,首日參與活動人數為![]() 人,以后每天人數比前一天都增加
人,以后每天人數比前一天都增加![]() ,
,![]() 天后捐步人數穩定在第
天后捐步人數穩定在第![]() 天的水平,假設此項活動的啟動資金為
天的水平,假設此項活動的啟動資金為![]() 萬元,每位捐步者每天可以使公司收益
萬元,每位捐步者每天可以使公司收益![]() 元(以下人數精確到
元(以下人數精確到![]() 人,收益精確到
人,收益精確到![]() 元).
元).
(1)求活動開始后第![]() 天的捐步人數,及前
天的捐步人數,及前![]() 天公司的捐步總收益;
天公司的捐步總收益;
(2)活動開始第幾天以后公司的捐步總收益可以收回啟動資金并有盈余?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓
,以原點為圓心,橢圓![]() 的短半軸長為半徑的圓與直線
的短半軸長為半徑的圓與直線![]() 相切.
相切.
(Ⅰ)求橢圓方程;
(Ⅱ)設![]() 為橢圓右頂點,過橢圓
為橢圓右頂點,過橢圓![]() 的右焦點的直線
的右焦點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點(異于
兩點(異于![]() ),直線
),直線![]() ,
,![]() 分別交直線
分別交直線![]() 于
于![]() ,
,![]() 兩點. 求證:
兩點. 求證:![]() ,
,![]() 兩點的縱坐標之積為定值.
兩點的縱坐標之積為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com