
【題目】已知橢圓![]() 離心率等于
離心率等于![]() ,
,![]() 、
、![]() 是橢圓上的兩點.
是橢圓上的兩點.
(1)求橢圓![]() 的方程;
的方程;
(2)![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側的動點.當
兩側的動點.當![]() 運動時,滿足
運動時,滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值?如果為定值,請求出此定值;如果不是定值,請說明理由.
的斜率是否為定值?如果為定值,請求出此定值;如果不是定值,請說明理由.
【答案】(1)![]() ;(2)定點
;(2)定點![]()
【解析】
(1)由題意列式關于a,b,c的方程組,求解可得a,b的值,則橢圓C的方程可求;
(2)設直線PA的斜率為k,則PB的斜率為﹣k,PA的直線方程為y﹣3=k(x﹣2)將直線的方程代入橢圓的方程,消去y得到關于x的一元二次方程,再結合根系數(shù)的關系利用弦長公式即可求得x1+2,同理PB的直線方程為y﹣3=﹣k(x﹣2),可得x2+2,從而得出AB的斜率為定值.
解:(1)由題意可得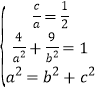 ,解得a=4,b
,解得a=4,b![]() ,c=2.
,c=2.
∴橢圓C的方程為![]() ;
;
(2)設A(x1,y1),B(x2,y2),
當∠APQ=∠BPQ,則PA、PB的斜率之和為0,設直線PA的斜率為k,
則PB的斜率為﹣k,直線PA的直線方程為y﹣3=k(x﹣2),
聯(lián)立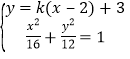 ,得(3+4k2)x2+8k(3﹣2k)x+4(3﹣2k)2﹣48=0.
,得(3+4k2)x2+8k(3﹣2k)x+4(3﹣2k)2﹣48=0.
∴![]() .
.
同理直線PB的直線方程為y﹣3=﹣k(x﹣2),
可得![]() .
.
∴![]() ,
,![]() ,
,
![]()
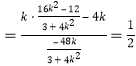 ,
,
∴AB的斜率為定值![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】甲烷分子由一個碳原子和四個氫原子組成,其空間構型為一個各條棱都相等的四面體,四個氫原子分別位于該四面體的四個頂點上,碳原子位于該四面體的中心,它與每個氫原子的距離都是![]() ,若將碳原子和氫原子均視為一個點,則任意兩個氫原子之間的距離為( )
,若將碳原子和氫原子均視為一個點,則任意兩個氫原子之間的距離為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)).在以坐標原點
為參數(shù)).在以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,且與直角坐標系長度單位相同的極坐標系中,曲線
軸的正半軸為極軸,且與直角坐標系長度單位相同的極坐標系中,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() .若直
.若直![]() 與曲線
與曲線![]() 相交于兩點
相交于兩點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線l1:3x﹣y﹣1=0,l2:x+2y﹣5=0,l3:x﹣ay﹣3=0不能圍成三角形,則實數(shù)a的取值可能為( )
A.1B.![]() C.﹣2D.﹣1
C.﹣2D.﹣1
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校為了了解學生使用手機的情況,分別在高一和高二兩個年級各隨機抽取了100名學生進行調查.下面是根據(jù)調查結果繪制的學生日均使用手機時間的頻數(shù)分布表和頻率分布直方圖,將使用手機時間不低于80分鐘的學生稱為“手機迷”.
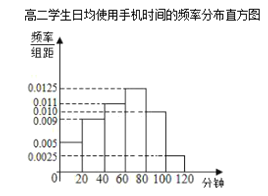
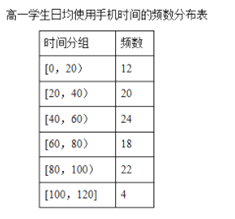
(I)將頻率視為概率,估計哪個年級的學生是“手機迷”的概率大?請說明理由.
(II)在高二的抽查中,已知隨機抽到的女生共有55名,其中10名為“手機迷”.根據(jù)已知條件完成下面的2×2列聯(lián)表,并據(jù)此資料你有多大的把握認為“手機迷”與性別有關?
非手機迷 | 手機迷 | 合計 | |
男 | |||
女 | |||
合計 |
附:隨機變量![]() (其中
(其中![]() 為樣本總量).
為樣本總量).
參考數(shù)據(jù) |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙兩位學生參加數(shù)學競賽培訓,現(xiàn)分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次,記錄如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)用莖葉圖表示這兩組數(shù)據(jù);
(2)現(xiàn)要從中選派一人參加數(shù)學競賽,從統(tǒng)計學的角度(平均數(shù)、方差)考慮,你認為選派哪位同學參加合適?請說明理由
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,則以下結論正確的是( )
,則以下結論正確的是( )
A.函數(shù)![]() 的單調減區(qū)間是
的單調減區(qū)間是![]()
B.函數(shù)![]() 有且只有1個零點
有且只有1個零點
C.存在正實數(shù)![]() ,使得
,使得![]() 成立
成立
D.對任意兩個正實數(shù)![]() ,
,![]() ,且
,且![]() ,若
,若![]() 則
則![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了解某校學生參加社區(qū)服務的情況,采用按性別分層抽樣的方法進行調查.已知該校共有學生960人,其中男生560人,從全校學生中抽取了容量為![]() 的樣本,得到一周參加社區(qū)服務的時間的統(tǒng)計數(shù)據(jù)好下表:
的樣本,得到一周參加社區(qū)服務的時間的統(tǒng)計數(shù)據(jù)好下表:
超過1小時 | 不超過1小時 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握認為該校學生一周參加社區(qū)服務時間是否超過1小時與性別有關?
(Ⅲ)以樣本中學生參加社區(qū)服務時間超過1小時的頻率作為該事件發(fā)生的概率,現(xiàn)從該校學生中隨機調查6名學生,試估計6名學生中一周參加社區(qū)服務時間超過1小時的人數(shù).
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com