
【題目】已知集合D={(x1,x2)|x1>0,x2>0,x1+x2=k}(其中k為正常數).
(1)設![]() ,求
,求![]() 的取值范圍
的取值范圍
(2)求證:當![]() 時,不等式
時,不等式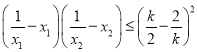 對任意
對任意![]() 恒成立
恒成立
(3)求使不等式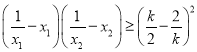 對任意
對任意![]() 恒成立的
恒成立的![]() 的范圍
的范圍
【答案】(1)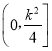 ;(2)見解析;(3)
;(2)見解析;(3)![]() .
.
【解析】
(1)利用基本不等式,其中和為定值,積有最大值;
(2)結合(1)中的范圍直接將左邊展開,利用u在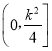 上單調遞增即可比較;
上單調遞增即可比較;
(3)結合(2)將(3)轉化為求使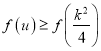 對
對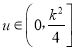 恒成立的
恒成立的![]() 的范圍,利用函數的單調性解決,或者作差法求解.
的范圍,利用函數的單調性解決,或者作差法求解.
(1)![]() ,當且僅當
,當且僅當![]() 時等號成立,
時等號成立,
故u的取值范圍為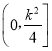 .
.
(2)![]()
由![]() ,又k≥1,k2﹣1≥0,
,又k≥1,k2﹣1≥0,
∴f(u)=u![]() 在
在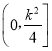 上是增函數
上是增函數
所以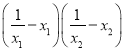

即當k≥1時不等式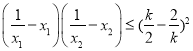 成立.
成立.
(3)
記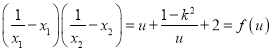 ,
,
則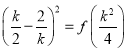 ,
,
即求使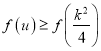 對
對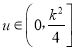 恒成立的k2的范圍.
恒成立的k2的范圍.
由(2)知,要使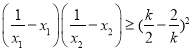
對任意(x1,x2)∈D恒成立,必有0<k<1,
因此1﹣k2>0,
∴函數![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,
要使函數f(u)在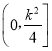 上恒有
上恒有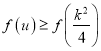 ,必有
,必有![]() ,即k4+16k2﹣16≤0,
,即k4+16k2﹣16≤0,
解得![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】通過隨機詢問110名性別不同的大學生是否愛好某項運動,得到如下的列聯表:
男 | 女 | 合計 | |
愛好 | 40 | 20 | 60 |
不愛好 | 20 | 30 | 50 |
合計 | 60 | 50 | 110 |
由K2=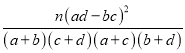 ,
,
附表:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
參照附表,得到的正確結論是( )
A.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
B.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關”
C.有99%以上的把握認為“愛好該項運動與性別有關”
D.有99%以上的把握認為“愛好該項運動與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() ,若對任意
,若對任意![]() ,滿足
,滿足![]() 且
且![]() (
(![]() 是與
是與![]() 無關的常數),則稱數列
無關的常數),則稱數列![]() 為
為![]() 數列.
數列.
(1)若![]() (
(![]() ),判斷數列
),判斷數列![]() 是否為
是否為![]() 數列,說明理由;
數列,說明理由;
(2)設![]() ,求證:數列
,求證:數列![]() 是
是![]() 數列,并求常數
數列,并求常數![]() 的取值范圍;
的取值范圍;
(3)設數列![]() (
(![]() ,
,![]() ),問數列
),問數列![]() 是否為
是否為![]() 數列?說明理由.
數列?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 滿足:①
滿足:①![]() ;②所有項
;②所有項![]() ;③
;③ ![]() .
.
設集合![]() ,將集合
,將集合![]() 中的元素的最大值記為
中的元素的最大值記為![]() .換句話說,
.換句話說, ![]() 是
是
數列![]() 中滿足不等式
中滿足不等式![]() 的所有項的項數的最大值.我們稱數列
的所有項的項數的最大值.我們稱數列![]() 為數列
為數列![]() 的
的
伴隨數列.例如,數列1,3,5的伴隨數列為1,1,2,2,3.
(1)若數列![]() 的伴隨數列為1,1,1,2,2,2,3,請寫出數列
的伴隨數列為1,1,1,2,2,2,3,請寫出數列![]() ;
;
(2)設![]() ,求數列
,求數列![]() 的伴隨數列
的伴隨數列![]() 的前100之和;
的前100之和;
(3)若數列![]() 的前
的前![]() 項和
項和![]() (其中
(其中![]() 常數),試求數列
常數),試求數列![]() 的伴隨數列
的伴隨數列![]() 前
前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為拋物線
為拋物線![]() 的焦點,點
的焦點,點![]() 在拋物線
在拋物線![]() 上,且
上,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
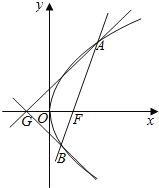
(2)已知點![]() ,延長
,延長![]() 交拋物線
交拋物線![]() 于點
于點![]() ,證明:以點
,證明:以點![]() 為圓心且與直線
為圓心且與直線![]() 相切的圓,必與直線
相切的圓,必與直線![]() 相切.
相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1為某省2018年1~4月快遞業務量統計圖,圖2是該省2018年1~4月快遞業務收入統計圖,下列對統計圖理解錯誤的是( )


A. 2018年1~4月的業務量,3月最高,2月最低,差值接近2000萬件
B. 2018年1~4月的業務量同比增長率均超過50%,在3月底最高
C. 從兩圖來看,2018年1~4月中的同一個月的快遞業務量與收入的同比增長率并不完全一致
D. 從1~4月來看,該省在2018年快遞業務收入同比增長率逐月增長
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com