
【題目】如圖,甲、乙兩個企業(yè)的用電負荷量![]() 關(guān)于投產(chǎn)持續(xù)時間
關(guān)于投產(chǎn)持續(xù)時間![]() (單位:小時)的關(guān)系
(單位:小時)的關(guān)系![]() 均近似地滿足函數(shù)
均近似地滿足函數(shù)![]() .
.
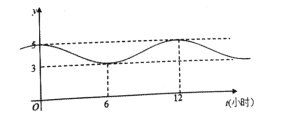
(1)根據(jù)圖象,求函數(shù)![]() 的解析式;
的解析式;
(2)為使任意時刻兩企業(yè)用電負荷量之和不超過9,現(xiàn)采用錯峰用電的方式,讓企業(yè)乙比企業(yè)甲推遲![]() 小時投產(chǎn),求
小時投產(chǎn),求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)4
;(2)4
【解析】
(1)由![]() ,得
,得![]() ,由
,由![]() ,得A,b,代入
,得A,b,代入![]() ,求得
,求得![]() ,從而即可得到本題答案;
,從而即可得到本題答案;
(2)由題,得![]() 恒成立,等價于
恒成立,等價于![]() 恒成立,然后利用和差公式展開,結(jié)合輔助角公式,逐步轉(zhuǎn)化,即可得到本題答案.
恒成立,然后利用和差公式展開,結(jié)合輔助角公式,逐步轉(zhuǎn)化,即可得到本題答案.
(1)解:由圖知![]() ,
,![]()
又![]() ,可得
,可得![]()
![]() ,代入
,代入![]() ,得
,得![]() ,
,
又![]() ,
,![]()
所求為![]()
(2)設(shè)乙投產(chǎn)持續(xù)時間為![]() 小時,則甲的投產(chǎn)持續(xù)時間為
小時,則甲的投產(chǎn)持續(xù)時間為![]() 小時,由誘導(dǎo)公式,企業(yè)乙用電負荷量隨持續(xù)時間
小時,由誘導(dǎo)公式,企業(yè)乙用電負荷量隨持續(xù)時間![]() 變化的關(guān)系式為:
變化的關(guān)系式為:
![]() 同理,企業(yè)甲用電負荷量變化關(guān)系式為:
同理,企業(yè)甲用電負荷量變化關(guān)系式為:
![]()
兩企業(yè)用電負荷量之和
![]() ,
,![]()
依題意,有![]() 恒成立
恒成立
即![]() 恒成立
恒成立
展開有![]() 恒成立
恒成立
![]()
其中, ,
, ,
,

整理得:![]()
解得![]()
即![]()
取![]() 得:
得:![]()
![]() 的最小值為4.
的最小值為4.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導(dǎo)學與測試系列答案
導(dǎo)學與測試系列答案科目:高中數(shù)學 來源: 題型:
【題目】 如圖是正方體的平面展開圖.在這個正方體中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四個命題中,正確命題的序號是________.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,已知四棱錐P-ABCD的底面為直角梯形,AB//DC,![]() ,PA
,PA![]() 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=![]() AB=1,M是PB的中點.
AB=1,M是PB的中點.
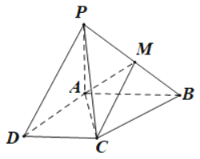
(1)證明:面PAD![]() 面PCD;
面PCD;
(2)求AC與PB所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,則當
,則當![]() 時,討論
時,討論![]() 單調(diào)性;
單調(diào)性;
(2)若![]() ,且當
,且當![]() 時,不等式
時,不等式![]() 在區(qū)間
在區(qū)間![]() 上有解,求實數(shù)
上有解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若![]() 是一個由數(shù)字1,2,3,4,5,6,7,8,9組成的
是一個由數(shù)字1,2,3,4,5,6,7,8,9組成的![]() 位正整數(shù),并同時滿足如下兩個條件:
位正整數(shù),并同時滿足如下兩個條件:
(1)數(shù)字1,2,…,![]() 在
在![]() 中各出現(xiàn)兩次;
中各出現(xiàn)兩次;
(2)每兩個相同的數(shù)字![]() 之間恰有
之間恰有![]() 個數(shù)字.
個數(shù)字.
此時,我們稱這樣的正整數(shù)![]() 為“好數(shù)”.例如,當
為“好數(shù)”.例如,當![]() 時,
時,![]() 可以是312 132.試確定滿足條件的正整數(shù)
可以是312 132.試確定滿足條件的正整數(shù)![]() 的值,并各寫出一個相應(yīng)的好數(shù)
的值,并各寫出一個相應(yīng)的好數(shù)![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】近年來,“共享單車”的出現(xiàn)為市民“綠色出行”提供了極大的方便,某共享單車公司“Mobike”計劃在甲、乙兩座城市共投資120萬元,根據(jù)行業(yè)規(guī)定,每個城市至少要投資40萬元,由前期市場調(diào)研可知:甲城市收益P與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,乙城市收益Q與投入
,乙城市收益Q與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,設(shè)甲城市的投入為
,設(shè)甲城市的投入為![]() (單位:萬元),兩個城市的總收益為
(單位:萬元),兩個城市的總收益為![]() (單位:萬元).
(單位:萬元).
(1)當甲城市投資50萬元時,求此時公司總收益;
(2)試問如何安排甲、乙兩個城市的投資,才能使總收益最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,內(nèi)角A,B,C的對邊分別為a,b,c,已知![]() .
.
(1)求角C的值;
(2)若c=2,且△ABC的面積為![]() ,求a,b.
,求a,b.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com