
【題目】已知數列![]() 滿足
滿足![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,寫出
,寫出![]() 所有可能的值;
所有可能的值;
(2)若數列![]() 是遞增數列,且
是遞增數列,且![]() 、
、![]() 、
、![]() 成等差數列,求p的值;
成等差數列,求p的值;
(3)若![]() ,且
,且![]() 是遞增數列,
是遞增數列,![]() 是遞減數列,求數列
是遞減數列,求數列![]() 的通項公式.
的通項公式.
【答案】(1)![]() 、
、![]() 、
、![]() 、
、![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由![]() ,
,![]() ,
,![]() ,分別取
,分別取![]() 、
、![]() 、
、![]() 即可得出
即可得出![]() 的所有可能取值;
的所有可能取值;
(2)由數列![]() 是遞增數列,得出
是遞增數列,得出![]() ,且有
,且有![]() ,得出
,得出![]() 、
、![]() 關于
關于![]() 的表達式,然后利用
的表達式,然后利用![]() 、
、![]() 、
、![]() 成等差數列得出關于
成等差數列得出關于![]() 的方程,解出即可;
的方程,解出即可;
(3)由數列![]() 是遞增數列得出
是遞增數列得出![]() ,可得
,可得![]() ,但
,但![]() ,可得出
,可得出![]() ,可得出
,可得出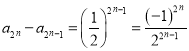 ,由數列
,由數列![]() 為遞減數列,同理可得
為遞減數列,同理可得![]() ,進而得到
,進而得到![]() ,再利用累加法可求出數列
,再利用累加法可求出數列![]() 的通項公式.
的通項公式.
(1)當![]() 時,
時,![]() ,則
,則![]() ,
,![]() ,
,![]() 或
或![]() .
.
當![]() 時,
時,![]() 或
或![]() ;當
;當![]() 時,
時,![]() 或
或![]() ;當
;當![]() 時,
時,![]() 或
或![]() .
.
因此,![]() 的所有可能取值有
的所有可能取值有![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(2)![]() 數列
數列![]() 是遞增數列,則
是遞增數列,則![]() ,則
,則![]() ,
,![]() ,
,
![]() ,同理得
,同理得![]() ,
,
由于![]() 、
、![]() 、
、![]() 成等差數列,則
成等差數列,則![]() ,即
,即![]() ,
,
整理得![]() ,
,![]() ,解得
,解得![]() ;
;
(3)![]() 數列
數列![]() 是遞增數列,所以
是遞增數列,所以![]() ,
,
即![]() ①,
①,
但![]() ,所以
,所以![]() ②,
②,
由①②知,![]() ,所以
,所以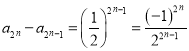 ③.
③.
![]() 數列
數列![]() 是遞減數列,同理可得
是遞減數列,同理可得![]() ,
,
所以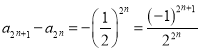 ④,
④,
由③④知,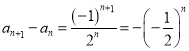 .
.
由累加法得![]()
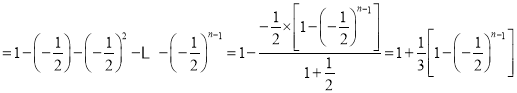
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設計一個隨機試驗,使一個事件的概率與某個未知數有關,然后通過重復試驗,以頻率估計概率,即可求得未知數的近似解,這種隨機試驗在數學上稱為隨機模擬法,也稱為蒙特卡洛法。比如要計算一個正方形內部不規則圖形的面積,就可以利用撒豆子,計算出落在不規則圖形內部和正方形內部的豆子數比近似等于不規則圖形面積與正方形面積比,從而近似求出不規則圖形的面積.
統計學上還有一個非常著名的蒲豐投針實驗:平面上間隔![]() 的平行線,向平行線間的平面上任意投擲一枚長為
的平行線,向平行線間的平面上任意投擲一枚長為![]() 的針
的針![]() ,通過多次實驗可以近似求出針與任一平行線(以
,通過多次實驗可以近似求出針與任一平行線(以![]() 為例)相交(當針的中點在平行線外不算相交)的概率.以
為例)相交(當針的中點在平行線外不算相交)的概率.以![]() 表示針的中點與最近一條平行線
表示針的中點與最近一條平行線![]() 的距離,又以
的距離,又以![]() 表示
表示![]() 與
與![]() 所成夾角,如圖甲,易知滿足條件:
所成夾角,如圖甲,易知滿足條件:![]() ,
,![]() .
.
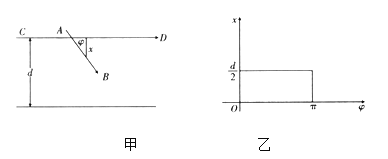
由這兩式可以確定平面上的一個矩形![]() ,如圖乙,在圖甲中,當
,如圖乙,在圖甲中,當![]() 滿足___________(
滿足___________(![]() 與
與![]() ,
,![]() 之間的關系)時,針與平行線相交(記為事件
之間的關系)時,針與平行線相交(記為事件![]() ).可用從實驗中獲得的頻率去近似
).可用從實驗中獲得的頻率去近似![]() ,即投針
,即投針![]() 次,其中相交的次數為
次,其中相交的次數為![]() ,則
,則![]() ,歷史上有一個數學家親自做了這實驗,他投擲的次數是5000,相交的次數為2550次,
,歷史上有一個數學家親自做了這實驗,他投擲的次數是5000,相交的次數為2550次,![]() ,
,![]() ,依據這個實驗求圓周率
,依據這個實驗求圓周率![]() 的近似值_________.(精確到3位小數)
的近似值_________.(精確到3位小數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將向量![]() =(
=(![]() ,
, ![]() ),
), ![]() =(
=(![]() ,
, ![]() ),…
),…![]() =(
=(![]() ,
,![]() )組成的系列稱為向量列{
)組成的系列稱為向量列{![]() },并定義向量列{
},并定義向量列{![]() }的前
}的前![]() 項和
項和![]() .如果一個向量列從第二項起,每一項與前一項的差都等于同一個向量,那么稱這樣的向量列為等差向量列。若向量列{
.如果一個向量列從第二項起,每一項與前一項的差都等于同一個向量,那么稱這樣的向量列為等差向量列。若向量列{![]() }是等差向量列,那么下述四個向量中,與
}是等差向量列,那么下述四個向量中,與![]() 一定平行的向量是 ( )
一定平行的向量是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
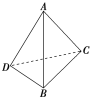
【題目】如圖,在三棱錐A-BCD中,AD⊥BD,AC⊥BC,∠DAB=![]() ,∠BAC=
,∠BAC=![]() .三棱錐的外接球的表面積為16π,則該三棱錐的體積的最大值為( )
.三棱錐的外接球的表面積為16π,則該三棱錐的體積的最大值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() .
.
(1)根據![]() 不同取值,討論函數
不同取值,討論函數![]() 的奇偶性;
的奇偶性;
(2)若![]() ,對于任意的
,對于任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若已知![]() ,
,![]() . 設函數
. 設函數![]() ,
,![]() ,存在
,存在![]() 、
、![]() ,使得
,使得![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com