
【題目】已知數(shù)列{an}的各項(xiàng)均為整數(shù),其前n項(xiàng)和為Sn.規(guī)定:若數(shù)列{an}滿足前r項(xiàng)依次成公差為1的等差數(shù)列,從第r﹣1項(xiàng)起往后依次成公比為2的等比數(shù)列,則稱數(shù)列{an}為“r關(guān)聯(lián)數(shù)列”.
(1)若數(shù)列{an}為“6關(guān)聯(lián)數(shù)列”,求數(shù)列{an}的通項(xiàng)公式;
(2)在(1)的條件下,求出Sn,并證明:對任意n∈N*,anSn≥a6S6;
(3)已知數(shù)列{an}為“r關(guān)聯(lián)數(shù)列”,且a1=﹣10,是否存在正整數(shù)k,m(m>k),使得a1+a2+…+ak﹣1+ak=a1+a2+…+am﹣1+am?若存在,求出所有的k,m值;若不存在,請說明理由.
【答案】(1)![]() (或
(或![]() )
)
(2)見解析;(3)存在![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
試題(1)若數(shù)列{an}為“6關(guān)聯(lián)數(shù)列”,{an}前6項(xiàng)為等差數(shù)列,從第5項(xiàng)起為等比數(shù)列,可得a6=a1+5,a5=a1+4,且![]() ,即
,即![]() ,解得a1,即可求數(shù)列{an}的通項(xiàng)公式;
,解得a1,即可求數(shù)列{an}的通項(xiàng)公式;
(2)由(1)得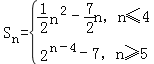 (或
(或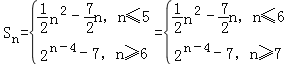 ,可見數(shù)列{anSn}的最小項(xiàng)為a6S6=﹣6,即可證明:對任意n∈N*,anSn≥a6S6;
,可見數(shù)列{anSn}的最小項(xiàng)為a6S6=﹣6,即可證明:對任意n∈N*,anSn≥a6S6;
(3)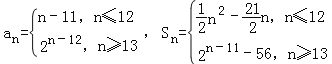 ,分類討論,求出所有的k,m值.
,分類討論,求出所有的k,m值.
解:(1)∵數(shù)列{an}為“6關(guān)聯(lián)數(shù)列”,
∴{an}前6項(xiàng)為等差數(shù)列,從第5項(xiàng)起為等比數(shù)列,
∴a6=a1+5,a5=a1+4,且![]() ,即
,即![]() ,解得a1=﹣3
,解得a1=﹣3
∴![]() (或
(或![]() )
)
(2)由(1)得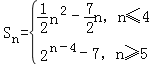 (或
(或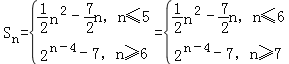 )
)
![]() ,
,
{Sn}:﹣3,﹣5,﹣6,﹣6,﹣5,﹣3,1,9,25,…{anSn}:9,10,6,0,﹣5,﹣6,4,72,400,…,
可見數(shù)列{anSn}的最小項(xiàng)為a6S6=﹣6,
證明: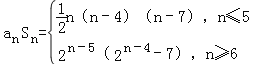 ,
,
列舉法知當(dāng)n≤5時,(anSn)min=a5S5=﹣5;
當(dāng)n≥6時,![]() ,設(shè)t=2n﹣5,則
,設(shè)t=2n﹣5,則![]() .
.
(3)數(shù)列{an}為“r關(guān)聯(lián)數(shù)列”,且a1=﹣10,∵![]()
∴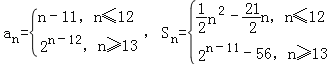
①當(dāng)k<m≤12時,由![]() 得(k+m)(k﹣m)=21(k﹣m)k+m=21,k,m≤12,m>k,∴
得(k+m)(k﹣m)=21(k﹣m)k+m=21,k,m≤12,m>k,∴![]() 或
或![]() .
.
②當(dāng)m>k>12時,由2k﹣11﹣56=2m﹣11﹣56得m=k,不存在
③當(dāng)k≤12,m>12時,由![]() ,2m﹣10=k2﹣21k+112
,2m﹣10=k2﹣21k+112
當(dāng)k=1時,2m﹣10=92,mN*;當(dāng)k=2時,2m﹣10=74,mN*;
當(dāng)k=3時,2m﹣10=58,mN*;當(dāng)k=4時,2m﹣10=44,mN*;
當(dāng)k=5時,2m﹣10=25,m=15∈N*;當(dāng)k=6時,2m﹣10=22,mN*;
當(dāng)k=7時,2m﹣10=14,mN*;當(dāng)k=8時,2m﹣10=23,m=13∈N*;
當(dāng)k=9時,2m﹣10=22,m=12舍去;當(dāng)k=10時,2m﹣10=2,m=11舍去
當(dāng)k=11時,2m﹣10=2,m=11舍去;當(dāng)k=12時,2m﹣10=22,m=12舍去
綜上所述,∴存在![]() 或
或![]() 或
或![]() 或
或![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列 ![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,對一切
,對一切![]() ,點(diǎn)
,點(diǎn)![]() 都在函數(shù)
都在函數(shù)![]() 的圖象上.
的圖象上.
(1)求![]() ,歸納數(shù)列
,歸納數(shù)列![]() 的通項(xiàng)公式(不必證明);
的通項(xiàng)公式(不必證明);
(2)將數(shù)列![]() 依次按1項(xiàng)、2項(xiàng)、3項(xiàng)、4項(xiàng)循環(huán)地分為
依次按1項(xiàng)、2項(xiàng)、3項(xiàng)、4項(xiàng)循環(huán)地分為![]() ,
,![]() ,
,![]() ,
, ![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分別計算各個括號內(nèi)各數(shù)之和,設(shè)由這些和按原來括號的前后順序構(gòu)成的數(shù)列為
,…,分別計算各個括號內(nèi)各數(shù)之和,設(shè)由這些和按原來括號的前后順序構(gòu)成的數(shù)列為![]() ,求
,求![]() 的值;
的值;
(3)設(shè)![]() 為數(shù)列
為數(shù)列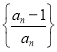 的前
的前![]() 項(xiàng)積,若不等式
項(xiàng)積,若不等式![]() 對一切
對一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)計算![]() ,
,![]() ,
,![]() ,
,![]() ,并求數(shù)列
,并求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)若數(shù)列![]() 滿足
滿足![]() ,求證:數(shù)列
,求證:數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(3)由數(shù)列![]() 的項(xiàng)組成一個新數(shù)列
的項(xiàng)組成一個新數(shù)列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,設(shè)
,設(shè)![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項(xiàng)和,試求
項(xiàng)和,試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在矩形![]() 中,
中,![]() ,
,![]() 為垂足,
為垂足,![]() 在
在![]() 上,將
上,將![]() 沿
沿![]() 折起,使點(diǎn)
折起,使點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的位置,連
的位置,連![]() ,且
,且![]() ,如圖2.
,如圖2.
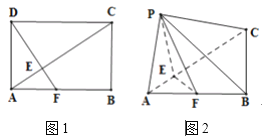
(1)求證:![]() 平面
平面![]() ;
;
(2)求鈍二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右焦點(diǎn)與短軸兩端點(diǎn)構(gòu)成一個面積為2的等腰直角三角形,
的右焦點(diǎn)與短軸兩端點(diǎn)構(gòu)成一個面積為2的等腰直角三角形,![]() 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)點(diǎn)![]() 在橢圓
在橢圓![]() 上,點(diǎn)
上,點(diǎn)![]() 在直線
在直線![]() 上,且
上,且![]() ,求證:
,求證:![]() 為定值;
為定值;
(3)設(shè)點(diǎn)![]() 在橢圓
在橢圓![]() 上運(yùn)動,
上運(yùn)動,![]() ,且點(diǎn)
,且點(diǎn)![]() 到直線
到直線![]() 的距離為常數(shù)
的距離為常數(shù)![]() ,求動點(diǎn)
,求動點(diǎn)![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】自然狀態(tài)下的魚類是一種可再生資源,為了持續(xù)利用這一資源,需從宏觀上考察其再生能力及捕撈強(qiáng)度對魚群總量的影響.用![]() 表示某魚群在第
表示某魚群在第![]() 年年初的總量且
年年初的總量且![]() .不考慮其他因素,設(shè)在第
.不考慮其他因素,設(shè)在第![]() 年內(nèi)魚群的繁殖量及捕撈量都與
年內(nèi)魚群的繁殖量及捕撈量都與![]() 成正比,死亡量與
成正比,死亡量與![]() 成正比,這些比例系數(shù)依次為正常數(shù)
成正比,這些比例系數(shù)依次為正常數(shù)![]() ,
,![]() ,
,![]()
(1)求![]() 與
與![]() 的關(guān)系式
的關(guān)系式
(2)若每年年初魚群的總量保持不變,求![]() ,
,![]() ,
,![]() ,
,![]() 所應(yīng)滿足的條件
所應(yīng)滿足的條件
(3)設(shè)![]() ,
,![]() ,為保證對任意
,為保證對任意![]() ,都有
,都有![]() ,則捕撈強(qiáng)度
,則捕撈強(qiáng)度![]() 的最大允許值是多少?并說明理由.
的最大允許值是多少?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)甲乙兩地相距100海里,船從甲地勻速駛到乙地,已知某船的最大船速是36海里/時:當(dāng)船速不大于每小時30海里/時,船每小時使用的燃料費(fèi)用和船速成正比;當(dāng)船速不小于每小時30海里/時,船每小時使用的燃料費(fèi)用和船速的平方成正比;當(dāng)船速為30海里/時,它每小時使用的燃料費(fèi)用為300元;其余費(fèi)用(不論船速為多少)都是每小時480元;
(1)試把每小時使用的燃料費(fèi)用P(元)表示成船速v(海里/時)的函數(shù);
(2)試把船從甲地行駛到乙地所需要的總費(fèi)用Y表示成船速v的函數(shù);
(3)當(dāng)船速為每小時多少海里時,船從甲地到乙地所需要的總費(fèi)用最少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,動點(diǎn)
中,動點(diǎn)![]() 到定點(diǎn)
到定點(diǎn)![]() 的距離與它到直線
的距離與它到直線![]() 的距離相等.
的距離相等.
(1)求動點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設(shè)動直線![]() 與曲線
與曲線![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,與直線
,與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() .
.
證明:以![]() 為直徑的圓恒過
為直徑的圓恒過![]() 軸上某定點(diǎn).
軸上某定點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a,b是不相等的兩個正數(shù),在a,b之間插入兩組實(shí)數(shù):x1,x2,…,xn和y1,y2,…,yn,(n∈N*,且n≥2),使得a,x1,x2,…,xn,b成等差數(shù)列,a,y1,y2,…,yn,b成等比數(shù)列,給出下列四個式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中一定成立的是( )
.其中一定成立的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com