【題目】重慶市推行“共享吉利博瑞車”服務，租用該車按行駛里程加用車時間收費，標準是“1元/公里
0.2元/分鐘”．剛在重慶參加工作的小劉擬租用“共享吉利博瑞車”上下班，同單位的鄰居老李告訴他：“上下班往返總路程雖然只有10公里，但偶爾開車上下班總共也需花費大約1小時”，并將自己近50天的往返開車的花費時間情況統計如表：
將老李統計的各時間段頻率視為相應概率，假定往返的路程不變，而且每次路上開車花費時間視為用車時間．
（1）試估計小劉每天平均支付的租車費用（每個時間段以中點時間計算）；
（2）小劉認為只要上下班開車總用時不超過45分鐘，租用“共享吉利博瑞車”為他該日的“最優選擇”，小劉擬租用該車上下班2天，設其中有
天為“最優選擇”，求
的分布列和數學期望．
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）用五點法畫出這個函數在一個周期內的圖像；（必須列表）
（2）求它的振幅、周期、初相、對稱軸方程；
（3）說明此函數圖象可由
在
上的圖象經過怎樣的變換得到.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，甲船由A島出發向北偏東45°的方向作勻速直線航行，速度為
nmile/h，在甲船從A島出發的同時，乙船從A島正南
nmile處的B島出發，朝北偏東30°的方向作勻速直線航行，速度為
nmile/h.
（1）若兩船能相遇，求m；
（2）當
時，兩船出發2小時后，求兩船之間的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
且
.圓C與直線
相切于點A，且點A的縱坐標為
，圓心C在直線
上.
（1）求直線
之間的距離；
（2）求圓C的標準方程；
（3）若直線
經過點
且與圓C交于
兩點，當△CPQ的面積最大時，求直線的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C1：
+
=1（a＞b＞0）的右焦點F（1，0），右準線l：x=4．圓C2：x2+y2=b2．A、B為橢圓上不同的兩點，AB中點為M．
（1）求橢圓C1的方程；
（2）若直線AB過F點，直線OM交l于N點，求證：NF⊥AB；
（3）若直線AB與圓C2相切，求原點O到AB中垂線的最大距離．
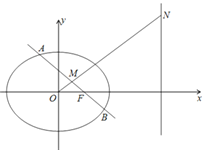
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近年來鄭州空氣污染較為嚴重，現隨機抽取一年（365天）內100天的空氣中
指數的監測數據，統計結果如下：
|
|
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 中度重污染 | 重度污染 |
天數 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
記某企業每天由空氣污染造成的經濟損失為
（單位：元），指數為
．當在區間
內時對企業沒有造成經濟損失；當在區間
內時對企業造成經濟損失成直線模型（當指數為150時造成的經濟損失為500元，當指數為200時，造成的經濟損失為700元）；當指數大于300時造成的經濟損失為2000元．
（1）試寫出
的表達式；
（2）試估計在本年內隨機抽取一天，該天經濟損失大于500元且不超過900元的概率；
（3）若本次抽取的樣本數據有30天是在供暖季，其中有8天為重度污染，完成下面列聯表，并判斷是否有
的把握認為鄭州市本年度空氣重度污染與供暖有關？
附：
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.828 |
，其中
．
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
是中心在原點，焦點在
軸上的雙曲線的右支，它的離心率剛好是其對應雙曲線的實軸長，且一條漸近線方程是
，線段
是過曲線右焦點
的一條弦，
是弦的中點。
（1）求曲線的方程；
（2）求點到
軸距離的最小值；
（3）若作出直線
，
使點在直線
上的射影
滿足
.當點
在曲線上運動時，求
的取值范圍.
（參考公式：若
為雙曲線
右支上的點，為右焦點，則
.（
為離心率））
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
