
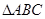 在平面
在平面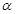 內(nèi),
內(nèi), ,
,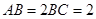 ,P為平面
,P為平面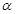 外一個動點,且PC=
外一個動點,且PC=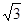 ,
,
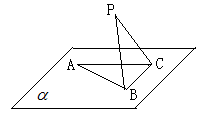
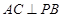
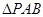 的面積取得最大值時,求直線BC與平面PAB所成角的大小
的面積取得最大值時,求直線BC與平面PAB所成角的大小 ;(2)
;(2)
 時,
時,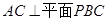 ,則
,則 ,由勾股定理可求得
,由勾股定理可求得 。(2)因為
。(2)因為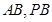 為定值,且
為定值,且 ,
,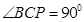 ,所以當(dāng)
,所以當(dāng)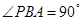 時,
時,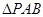 的面積取得最大值。分析可知
的面積取得最大值。分析可知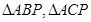 均是以
均是以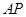 為底的等腰三角形,故取
為底的等腰三角形,故取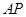 中點
中點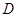 ,連接
,連接 。則有
。則有 ,從而可得
,從而可得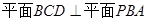 ,可知
,可知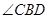 就是直線
就是直線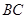 與平面PAB所成角,在
與平面PAB所成角,在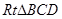 中可求此角。
中可求此角。 ,所以
,所以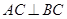 ,當(dāng)
,當(dāng) 時,
時,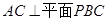 ,而
,而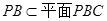 ,所以
,所以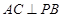 ,此時,
,此時,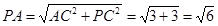 ,即當(dāng)PA=
,即當(dāng)PA= 時,
時,
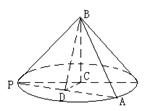
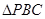 中,因為PC=
中,因為PC=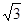 ,
, ,
,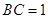 ,所以
,所以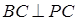 ,當(dāng)
,當(dāng)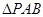 的面積取得最大值時,
的面積取得最大值時,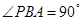 ,(如圖)在
,(如圖)在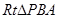 中,因為
中,因為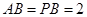 ,取
,取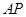 中點
中點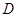 ,連接
,連接 。則
。則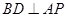 ,因為
,因為 且點
且點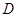 為
為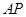 中點,所以
中點,所以 ,因為
,因為 ,所以
,所以 ,由此可求得
,由此可求得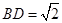 ,又在
,又在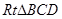 中,
中,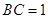 ,所以
,所以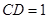 ,由于
,由于 ,所以
,所以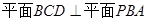 ,所以
,所以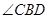 就是直線
就是直線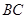 與平面PAB所成角,在
與平面PAB所成角,在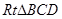 中,因為
中,因為 ,所以
,所以 ,所以直線BC與平面
,所以直線BC與平面 所成角的大小為
所成角的大小為


科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
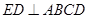 ,ED=1,
,ED=1,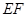 //BD,且
//BD,且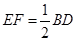 .
.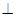 平面BDEF;
平面BDEF;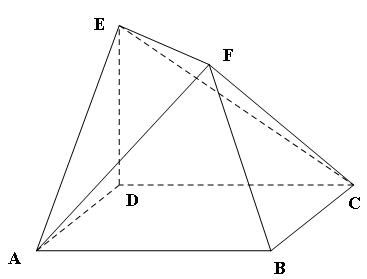
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
 分別是正方體
分別是正方體 的棱
的棱 的中點,點
的中點,點 分別是線段
分別是線段 與
與 上的點,則與平面
上的點,則與平面 垂直的直線
垂直的直線 有( )
有( )| A.0條 | B.1條 | C.2條 | D.無數(shù)條 |

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
A.過平面 外一點可以作無數(shù)條直線與平面 外一點可以作無數(shù)條直線與平面 平行 平行 |
| B.與同一個平面所成的角相等的兩條直線必平行 |
C.若直線 垂直平面 垂直平面 內(nèi)的兩條相交直線,則直線 內(nèi)的兩條相交直線,則直線 必垂直平面 必垂直平面 |
| D.垂直于同一個平面的兩條直線平行 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
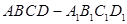 中,線段
中,線段 上(不包括端點)各有一點
上(不包括端點)各有一點 ,且
,且 ,下列說法中,不正確的是( )
,下列說法中,不正確的是( ) 四點共面
四點共面 與平面
與平面 所成的角為定值
所成的角為定值
 的大小為
的大小為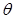 ,則
,則 的最小值為
的最小值為
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com