
【題目】若直線(xiàn)![]() 與曲線(xiàn)
與曲線(xiàn)![]() 滿(mǎn)足下列兩個(gè)條件:①直線(xiàn)
滿(mǎn)足下列兩個(gè)條件:①直線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 處與曲線(xiàn)
處與曲線(xiàn)![]() 相切;②曲線(xiàn)
相切;②曲線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 附近位于直線(xiàn)
附近位于直線(xiàn)![]() 的兩側(cè),則稱(chēng)直線(xiàn)
的兩側(cè),則稱(chēng)直線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 處“切過(guò)”曲線(xiàn)
處“切過(guò)”曲線(xiàn)![]() .則下列結(jié)論正確的是( )
.則下列結(jié)論正確的是( )
A.直線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 處“切過(guò)”曲線(xiàn)
處“切過(guò)”曲線(xiàn)![]()
B.直線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 處“切過(guò)”曲線(xiàn)
處“切過(guò)”曲線(xiàn)![]()
C.直線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 處“切過(guò)”曲線(xiàn)
處“切過(guò)”曲線(xiàn)![]()
D.直線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 處“切過(guò)”曲線(xiàn)
處“切過(guò)”曲線(xiàn)![]()
【答案】ACD
【解析】
根據(jù)“切過(guò)”的定義以及導(dǎo)數(shù)的幾何意義逐個(gè)選項(xiàng)判定即可.
A項(xiàng),因?yàn)?/span>![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,
,
所以![]() 是曲線(xiàn)
是曲線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線(xiàn).
處的切線(xiàn).
當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ,
,
所以曲線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 附近位于直線(xiàn)
附近位于直線(xiàn)![]() 的兩側(cè),結(jié)論正確;
的兩側(cè),結(jié)論正確;
B項(xiàng),![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,在
,在![]() 處的切線(xiàn)為
處的切線(xiàn)為![]() .
.
令![]() ,則
,則![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ,
,
所以![]() .故
.故![]() ,
,
即當(dāng)![]() 時(shí),曲線(xiàn)
時(shí),曲線(xiàn)![]() 全部位于直線(xiàn)
全部位于直線(xiàn)![]() 的下側(cè)(除切點(diǎn)外),結(jié)論錯(cuò)誤;
的下側(cè)(除切點(diǎn)外),結(jié)論錯(cuò)誤;
C項(xiàng),![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,在
,在![]() 處的切線(xiàn)為
處的切線(xiàn)為![]() ,
,
由正弦函數(shù)圖像可知,曲線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 附近位于直線(xiàn)
附近位于直線(xiàn)![]() 的兩側(cè),結(jié)論正確;
的兩側(cè),結(jié)論正確;
D項(xiàng),![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,在
,在![]() 處的切線(xiàn)為
處的切線(xiàn)為![]() ,
,
由正切函數(shù)圖像可知,曲線(xiàn)![]() 在點(diǎn)
在點(diǎn)![]() 附近位于直線(xiàn)
附近位于直線(xiàn)![]() 的兩側(cè),結(jié)論正確.
的兩側(cè),結(jié)論正確.
故選:ACD.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司計(jì)劃購(gòu)買(mǎi)1臺(tái)機(jī)器,該種機(jī)器使用三年后即被淘汰.在購(gòu)進(jìn)機(jī)器時(shí),可以一次性額外購(gòu)買(mǎi)![]() 次維修,每次維修費(fèi)用300元,另外實(shí)際維修一次還需向維修人員支付上門(mén)服務(wù)費(fèi)80元.在機(jī)器使用期間,如果維修次數(shù)超過(guò)購(gòu)買(mǎi)的
次維修,每次維修費(fèi)用300元,另外實(shí)際維修一次還需向維修人員支付上門(mén)服務(wù)費(fèi)80元.在機(jī)器使用期間,如果維修次數(shù)超過(guò)購(gòu)買(mǎi)的![]() 次時(shí),則超出的維修次數(shù),每次只需支付維修費(fèi)用700元,無(wú)需支付上門(mén)服務(wù)費(fèi).需決策在購(gòu)買(mǎi)機(jī)器時(shí)應(yīng)同時(shí)一次性購(gòu)買(mǎi)幾次維修,為此搜集并整理了100臺(tái)這種機(jī)器在三年使用期內(nèi)的維修次數(shù),得到下面統(tǒng)計(jì)表:
次時(shí),則超出的維修次數(shù),每次只需支付維修費(fèi)用700元,無(wú)需支付上門(mén)服務(wù)費(fèi).需決策在購(gòu)買(mǎi)機(jī)器時(shí)應(yīng)同時(shí)一次性購(gòu)買(mǎi)幾次維修,為此搜集并整理了100臺(tái)這種機(jī)器在三年使用期內(nèi)的維修次數(shù),得到下面統(tǒng)計(jì)表:
維修次數(shù) | 6 | 7 | 8 | 9 | 10 |
頻數(shù) | 10 | 20 | 30 | 30 | 10 |
記![]() 表示1臺(tái)機(jī)器在三年使用期內(nèi)的維修次數(shù),
表示1臺(tái)機(jī)器在三年使用期內(nèi)的維修次數(shù),![]() 表示1臺(tái)機(jī)器維修所需的總費(fèi)用(單位:元).
表示1臺(tái)機(jī)器維修所需的總費(fèi)用(單位:元).
(1)若![]() ,求
,求![]() 與
與![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)假設(shè)這100臺(tái)機(jī)器在購(gòu)機(jī)的同時(shí)每臺(tái)都購(gòu)買(mǎi)8次維修,或每臺(tái)都購(gòu)買(mǎi)9次維修,分別計(jì)算這100臺(tái)機(jī)器在維修上所需總費(fèi)用的平均數(shù),并以此作為決策依據(jù),購(gòu)買(mǎi)1臺(tái)機(jī)器的同時(shí)應(yīng)購(gòu)買(mǎi)8次還是9次維修?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
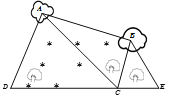
【題目】如圖,為了測(cè)量某濕地![]() 兩點(diǎn)間的距離,觀察者找到在同一直線(xiàn)上的三點(diǎn)
兩點(diǎn)間的距離,觀察者找到在同一直線(xiàn)上的三點(diǎn)![]() .從
.從![]() 點(diǎn)測(cè)得
點(diǎn)測(cè)得![]() ,從
,從![]() 點(diǎn)測(cè)得
點(diǎn)測(cè)得![]() ,
,![]() ,從
,從![]() 點(diǎn)測(cè)得
點(diǎn)測(cè)得![]() .若測(cè)得
.若測(cè)得![]() ,
,![]() (單位:百米),則
(單位:百米),則![]() 兩點(diǎn)的距離為( )
兩點(diǎn)的距離為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為慶祝黨的98歲生日,某高校組織了“歌頌祖國(guó),緊跟黨走”為主題的黨史知識(shí)競(jìng)賽。從參加競(jìng)賽的學(xué)生中,隨機(jī)抽取40名學(xué)生,將其成績(jī)分為六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如圖所示的頻率分布直方圖.
,到如圖所示的頻率分布直方圖.

(1)求圖中![]() 的值及樣本的中位數(shù)與眾數(shù);
的值及樣本的中位數(shù)與眾數(shù);
(2)若從競(jìng)賽成績(jī)?cè)?/span>![]() 與
與![]() 兩個(gè)分?jǐn)?shù)段的學(xué)生中隨機(jī)選取兩名學(xué)生,設(shè)這兩名學(xué)生的競(jìng)賽成績(jī)之差的絕對(duì)值不大于
兩個(gè)分?jǐn)?shù)段的學(xué)生中隨機(jī)選取兩名學(xué)生,設(shè)這兩名學(xué)生的競(jìng)賽成績(jī)之差的絕對(duì)值不大于![]() 分為事件
分為事件![]() ,求事件
,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在一場(chǎng)拋擲骰子的游戲中,游戲者最多有三次機(jī)會(huì)拋擲一顆骰子,游戲規(guī)則如下:拋擲1枚骰子,第1次拋擲骰子向上的點(diǎn)數(shù)為奇數(shù)則記為成功,第2次拋擲骰子向上的點(diǎn)數(shù)為3的倍數(shù)則記為成功,第3次拋擲骰子向上的點(diǎn)數(shù)為6則記為成功.游戲者在前兩次拋擲中至少成功一次才可以進(jìn)行第三次拋擲,其中拋擲骰子不成功得0分,第1次成功得3分,第2次成功得3分,第3次成功得4分.
(1)求游戲者有機(jī)會(huì)第3次拋擲骰子的概率;
(2)設(shè)游戲者在一場(chǎng)拋擲骰子游戲中所得的分?jǐn)?shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知集合![]() .
.
(1)求證:函數(shù)![]() ;
;
(2)某同學(xué)由(1)又發(fā)現(xiàn)![]() 是周期函數(shù)且是偶函數(shù),于是他得出兩個(gè)命題:①集合
是周期函數(shù)且是偶函數(shù),于是他得出兩個(gè)命題:①集合![]() 中的元素都是周期函數(shù);②集合
中的元素都是周期函數(shù);②集合![]() 中的元素都是偶函數(shù),請(qǐng)對(duì)這兩個(gè)命題給出判斷,如果正確,請(qǐng)證明;如果不正確,請(qǐng)舉出反例;
中的元素都是偶函數(shù),請(qǐng)對(duì)這兩個(gè)命題給出判斷,如果正確,請(qǐng)證明;如果不正確,請(qǐng)舉出反例;
(3)設(shè)![]() 為非零常數(shù),求
為非零常數(shù),求![]() 的充要條件,并給出證明.
的充要條件,并給出證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知正項(xiàng)數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]() ,
,![]() ,數(shù)列
,數(shù)列![]() 滿(mǎn)足
滿(mǎn)足![]() ,且
,且![]()
(I)求數(shù)列![]() ,
,![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(II)令![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】過(guò)直線(xiàn)2x+y+4=0和圓x2+y2+2x﹣4y+1=0的交點(diǎn),且面積最小的圓方程為( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com