
【題目】已知三點(diǎn)A(-1,1,2),B(1,2,-1),C(a,0,3),是否存在實(shí)數(shù)a,使A、B、C共線?若存在,求出a的值;若不存在,說明理由.
【答案】不存在實(shí)數(shù)a,使A、B、C共線
【解析】試題分析: 根據(jù)三點(diǎn)共線時線段關(guān)系分類列式BC=AC+AB或AC=BC+AB,利用兩點(diǎn)間距離公式代入化簡,根據(jù)方程解的情況確定是否存在
試題解析:AB=![]() =
=![]() ,
,
AC=![]() =
=![]() ,
,
BC=![]()
=![]() ,
,
因?yàn)?/span>BC>AB,所以,若A,B,C三點(diǎn)共線,有BC=AC+AB或AC=BC+AB,
若BC=AC+AB,整理得:5a2+18a+19=0,
此方程無解;
若AC=BC+AB,整理得:5a2+18a+19=0,此方程也無解.
所以不存在實(shí)數(shù)a,使A、B、C共線.
點(diǎn)睛: ![]() 兩點(diǎn)間距離公式為
兩點(diǎn)間距離公式為![]()


 互動英語系列答案
互動英語系列答案 名牌學(xué)校分層周周測系列答案
名牌學(xué)校分層周周測系列答案 黃岡海淀全程培優(yōu)測試卷系列答案
黃岡海淀全程培優(yōu)測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的定義域是
的定義域是![]() .
.
(1)判斷![]() 在
在![]() 上的單調(diào)性,并證明;
上的單調(diào)性,并證明;
(2)若不等式![]() 對任意
對任意![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,左頂點(diǎn)為
,左頂點(diǎn)為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn), ![]() 是橢圓
是橢圓![]() 上的兩點(diǎn),連接
上的兩點(diǎn),連接![]() 的直線平行
的直線平行![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,證明:
,證明: ![]() 成等比數(shù)列.
成等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
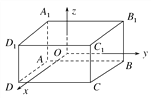
【題目】如圖,已知長方體ABCD-A1B1C1D1的對稱中心在坐標(biāo)原點(diǎn),交于同一頂點(diǎn)的三個面分別平行于三個坐標(biāo)平面,頂點(diǎn)A(-2,-3,-1),求其他七個頂點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C:x2+y2-8y+12=0,直線l經(jīng)過點(diǎn)D(-2,0),且斜率為k.
(1)求以線段CD為直徑的圓E的方程.
(2)若直線l與圓C相離,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】直線l經(jīng)過兩直線l1:2x-y+4=0與l2:x-y+5=0的交點(diǎn),且與直線x-2y-6=0垂直.
(1)求直線l的方程.
(2)若點(diǎn)P(a,1)到直線l的距離為![]() ,求實(shí)數(shù)a的值.
,求實(shí)數(shù)a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)人的某一特征(如眼睛的大小)是由他的一對基因所決定,以d表示顯性基因,r表示隱性基因,則具有dd基因的人為純顯性,具有rr基因的人為純隱性,具有rd基因的人為混合性,純顯性與混合性的人都顯露顯性基因決定的某一特征,孩子從父母身上各得到一個基因,假定父母都是混合性,問:
(1)1個孩子顯露顯性特征的概率是多少?
(2)“該父母生的2個孩子中至少有1個顯露顯性特征”,這種說法正確嗎?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com