
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,面
,面![]() 面
面![]() ,
,![]() 為
為![]() 的中點.
的中點.
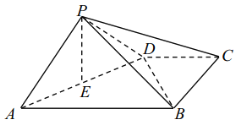
(1)求證:![]() ;
;
(2)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 面
面![]() ?若存在,請證明你的結論;若不存在,請說明理由.
?若存在,請證明你的結論;若不存在,請說明理由.
科目:高中數學 來源: 題型:
【題目】根據全球摩天大樓的統計,至2019年,安徽省合肥市的摩天大樓已經有95座在中國城市中排名第10位,全球排名第15位,目前合肥恒大中心建設中的最高樓,外形設計成了“竹節”的形態,既體現了力量超凡,又象征著向上生長的強烈意志,更預示了未來的繁榮和興旺.它與傳承千年的“微文化”相得益建成后將躋身世界十大摩天大樓之列,若大樓由9節“竹節”組成,最上部分的4節高228米,最下部分3節高204米,且每一節高度變化均勻(即每節高度自上而下成等差數列),則該摩天大樓的總高度為( )
A.518米B.558米C.588米D.668米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年12月以來,湖北省武漢市持續開展流感及相關疾病監測,發現多起病毒性肺炎病例,均診斷為病毒性肺炎/肺部感染,后被命名為新型冠狀病毒肺炎(CoronaVirusDisease2019,COVID—19),簡稱“新冠肺炎”.下圖是2020年1月15日至1月24日累計確診人數隨時間變化的散點圖.
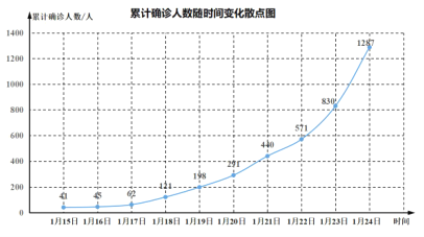
為了預測在未釆取強力措施下,后期的累計確診人數,建立了累計確診人數y與時間變量t的兩個回歸模型,根據1月15日至1月24日的數據(時間變量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() 哪一個適宜作為累計確診人數y與時間變量t的回歸方程類型?(給出判斷即可,不必說明理由)
哪一個適宜作為累計確診人數y與時間變量t的回歸方程類型?(給出判斷即可,不必說明理由)
(2根據(1)的判斷結果及附表中數據,建立y關于x的回歸方程;
(3)以下是1月25日至1月29日累計確診人數的真實數據,根據(2)的結果回答下列問題:
時間 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累計確診人數的真實數據 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)當1月25日至1月27日這3天的誤差(模型預測數據與真實數據差值的絕對值與真實數據的比值)都小于0.1則認為模型可靠,請判斷(2)的回歸方程是否可靠?
(ⅱ)2020年1月24日在人民政府的強力領導下,全國人民共同采取了強力的預防“新冠肺炎”的措施,若采取措施5天后,真實數據明顯低于預測數據,則認為防護措施有效,請判斷預防措施是否有效?
附:對于一組數據(![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為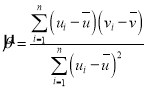 ,
,![]() .
.
參考數據:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
, ![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將曲線![]() 的極坐標方程化為直角坐標方程,并說明曲線
的極坐標方程化為直角坐標方程,并說明曲線![]() 的形狀;
的形狀;
(2)若直線![]() 經過點
經過點![]() ,求直線
,求直線![]() 被曲線
被曲線![]() 截得的線段的長.
截得的線段的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年,中國的國內生產總值(GDP)已經達到100億元人民幣,位居世界第二,這其中實體經濟的貢獻功不可沒,實體經濟組織一般按照市場化原則運行,某生產企業一種產品的成本由原料成本及非原料成本組成,每件產品的非原料成本![]() (元)與生產該產品的數量
(元)與生產該產品的數量![]() (千件)有關,經統計得到如下數據:
(千件)有關,經統計得到如下數據:

根據以上數據繪制了如下的散點圖
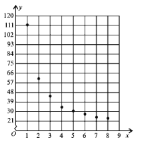
現考慮用反比例函數模型![]() 和指數函數模型
和指數函數模型![]() 分別對兩個變量關系進行擬合,為此變換如下:令
分別對兩個變量關系進行擬合,為此變換如下:令![]() ,則
,則![]() ,即
,即![]() 與
與![]() 也滿足線性關系,令
也滿足線性關系,令![]() ,則
,則![]() ,即
,即![]() 也滿足線線關系,這樣就可以使用最小二乘法求得非線性回歸方程,已求得用指數函數模型擬合的回歸方程為
也滿足線線關系,這樣就可以使用最小二乘法求得非線性回歸方程,已求得用指數函數模型擬合的回歸方程為![]() 與
與![]() 的相關系數
的相關系數![]() ,其他參考數據如下(其中
,其他參考數據如下(其中![]() )
)

(1)求指數函數模型和反比例函數模型中![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)試計算![]() 與
與![]() 的相關系數
的相關系數![]() ,并用相關系數判斷:選擇反比例函數和指數函數兩個模型中哪一個擬合效果更好(精確到0.01)?
,并用相關系數判斷:選擇反比例函數和指數函數兩個模型中哪一個擬合效果更好(精確到0.01)?
(3)根據(2)小題的選擇結果,該企業采用訂單生產模式(即根據訂單數量進行生產,產品全部售出),根據市場調研數據,該產品定價為100元時得到簽到訂單的情況如下表:
訂單數(千件) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
概率 |
|
|
|
|
|
|
|
|
|
|
|
已知每件產品的原來成本為10元,試估算企業的利潤是多少?(精確到1千元)
參考公式:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別是:
的斜率和截距的最小二乘估計分別是: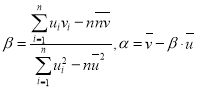 相關系數:
相關系數: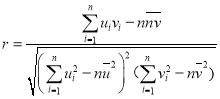
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①![]() ;②
;②![]() ,這兩個條件中任選一個,補充在下面問題中,然后解答補充完整的題目.
,這兩個條件中任選一個,補充在下面問題中,然后解答補充完整的題目.
在![]() 中,內角
中,內角![]() 的對邊分別為
的對邊分別為![]() ,設
,設![]() 的面積為
的面積為![]() ,已知 .
,已知 .
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
注:如果選擇多個條件分別解答,按第一個解答計分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程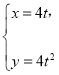 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,已知曲線C2的極坐標方程為ρ=4sinθ.
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,已知曲線C2的極坐標方程為ρ=4sinθ.
(1)求C1的直角坐標方程與C2的直角坐標方程;
(2)已知射線![]() 與C1交于O,P兩點,與C2交于O,Q兩點,且Q為OP的中點,求α.
與C1交于O,P兩點,與C2交于O,Q兩點,且Q為OP的中點,求α.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com