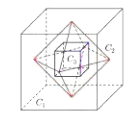
【題目】如圖，記棱長為1的正方體
，以各個面的中心為頂點的正八面體為
，以各面的中心為頂點的正方體為
，以各個面的中心為頂點的正八面體為
，……，以此類推得一系列的多面體
，設(shè)的棱長為
，則數(shù)列
的各項和為________.
【答案】
【解析】
根據(jù)條件求出
，
，
，
，然后歸納得到：奇數(shù)項與偶數(shù)項都是等比數(shù)列，然后求和即可.
正方體
各面中心為頂點的凸多面體
為正八面體，
它的中截面（垂直平分對頂點連線的界面）是正方形，
該正方形對角線的長度等于正方體的棱長，
所以
，
以各個面的中心為頂點的凸多面體
為正方體，
正方體面對角線長等于棱長的
，（正三角形中心到對邊的距離等于高的），
因此對角線為
，所以
，
以上方式類推得到
，
，
，
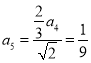所以
各項為
，
奇數(shù)項是以
為首項，以
為公比的等比數(shù)列，
偶數(shù)項是以
為首項，以為公比的等比數(shù)列，
所以數(shù)列的各項和為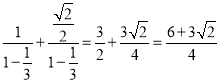
.
故答案為：.
能力評價系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知焦點在x軸上的雙曲線C的兩條漸近線過坐標(biāo)原點，且兩條漸近線與以點
為圓心，1為半徑的圓相切，又知C的一個焦點與P關(guān)于直線
對稱.
（1）求雙曲線C的方程；
（2）設(shè)直線
與雙曲線C的左支交于A、B兩點，另一直線
經(jīng)過
及AB的中點，求直線在y軸上的截距b的取值范圍；
（3）若Q是雙曲線C上的任一點，
、
為雙曲線C的左、右兩個焦點，從引
的角平分線的垂線，垂足為N，試求點N的軌跡方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】足球是世界普及率最高的運動，我國大力發(fā)展校園足球.為了解本地區(qū)足球特色學(xué)校的發(fā)展?fàn)顩r，社會調(diào)查小組得到如下統(tǒng)計數(shù)據(jù)：
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色學(xué)校y（百個） | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（1）根據(jù)上表數(shù)據(jù)，計算y與x的相關(guān)系數(shù)r，并說明y與x的線性相關(guān)性強弱.
（已知：
，則認(rèn)為y與x線性相關(guān)性很強；
，則認(rèn)為y與x線性相關(guān)性一般；
，則認(rèn)為y與x線性相關(guān)性較）：
（2）求y關(guān)于x的線性回歸方程，并預(yù)測A地區(qū)2020年足球特色學(xué)校的個數(shù)（精確到個）.
參考公式和數(shù)據(jù)：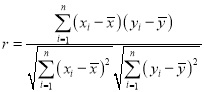
，
，
.
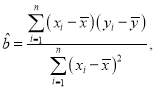
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】（理）已知數(shù)列
滿足
（
），首項
．
（1）求數(shù)列的通項公式；
（2）求數(shù)列的前
項和
；
（3）數(shù)列
滿足
，記數(shù)列
的前項和為
，
是△ABC的內(nèi)角，若
對于任意
恒成立，求角的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某班學(xué)生中喜愛看綜藝節(jié)目的有18人，體育節(jié)目的有27人，時政節(jié)目的有9人，現(xiàn)采取分層抽樣的方法從這些學(xué)生中抽取6名學(xué)生．
（Ⅰ）求應(yīng)從喜愛看綜藝節(jié)目，體育節(jié)目，時政節(jié)目的學(xué)生中抽取的學(xué)生人數(shù)；
（Ⅱ）若從抽取的6名學(xué)生中隨機抽取2人分作一組，
（1）列出所有可能的結(jié)果；
（2）求抽取的2人中有1人喜愛綜藝節(jié)目1人喜愛體育節(jié)目的概率．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某企業(yè)參加
項目生產(chǎn)的工人為
人，平均每人每年創(chuàng)造利潤
萬元.根據(jù)現(xiàn)實的需要，從項目中調(diào)出
人參與
項目的售后服務(wù)工作，每人每年可以創(chuàng)造利潤
萬元（
），項目余下的工人每人每年創(chuàng)造利圖需要提高
（1）若要保證項目余下的工人創(chuàng)造的年總利潤不低于原來名工人創(chuàng)造的年總利潤，則最多調(diào)出多少人參加項目從事售后服務(wù)工作？
（2）在（1）的條件下，當(dāng)從項目調(diào)出的人數(shù)不能超過總?cè)藬?shù)的
時，才能使得項目中留崗工人創(chuàng)造的年總利潤始終不低于調(diào)出的工人所創(chuàng)造的年總利潤，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某公司生產(chǎn)的某批產(chǎn)品的銷售量
萬件（生產(chǎn)量與銷售量相等）與促銷費用
萬元滿足
（其中
，
為正常數(shù)）．已知生產(chǎn)該產(chǎn)品還需投入成本
萬元（不含促銷費用），產(chǎn)品的銷售價格定為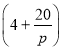
元
件．
（1）將該產(chǎn)品的利潤
萬元表示為促銷費用萬元的函數(shù)；
（2）促銷費用投入多少萬元時，該公司的利潤最大？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如下圖是某校高三（1）班的一次數(shù)學(xué)知識競賽成績的莖葉圖（圖中僅列出
，
的數(shù)據(jù)）和頻率分布直方圖.
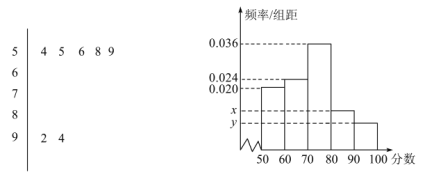
（1）求分?jǐn)?shù)在的頻率及全班人數(shù)；
（2）求頻率分布直方圖中的
；
（3）若要從分?jǐn)?shù)在
之間的試卷中任取兩份分析學(xué)生失分情況，求在抽取的試卷中，至少有一份分?jǐn)?shù)在之間的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
