
【題目】一個(gè)袋子中有紅、黃、藍(lán)、綠四個(gè)小球,有放回地從中任取一個(gè)小球,將“三次抽取后,紅色小球,黃色小球都取到”記為事件M,用隨機(jī)模擬的方法估計(jì)事件M發(fā)生的概率.利用電腦隨機(jī)產(chǎn)生整數(shù)0,1,2,3四個(gè)隨機(jī)數(shù),分別代表紅、黃、藍(lán)、綠四個(gè)小球,以每三個(gè)隨機(jī)數(shù)為一組,表示取小球三次的結(jié)果,經(jīng)隨機(jī)模擬產(chǎn)生了以下18組隨機(jī)數(shù):
110 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估計(jì)事件M發(fā)生的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
估計(jì)事件![]() 發(fā)生的隨機(jī)數(shù)有6個(gè),由此可以估計(jì)事件
發(fā)生的隨機(jī)數(shù)有6個(gè),由此可以估計(jì)事件![]() 發(fā)生的概率.
發(fā)生的概率.
利用電腦隨機(jī)產(chǎn)生整數(shù)0,1,2,3四個(gè)隨機(jī)數(shù),分別代表“紅、黃、藍(lán)、綠”這四個(gè)小球,
以每三個(gè)隨機(jī)數(shù)為一組,表示取小球三次的結(jié)果,經(jīng)隨機(jī)模擬產(chǎn)生了以下18組隨機(jī)數(shù):
110 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
估計(jì)事件![]() 發(fā)生的隨機(jī)數(shù)有:
發(fā)生的隨機(jī)數(shù)有:
110,021,001,130,031,103,共6個(gè),
由此可以估計(jì)事件![]() 發(fā)生的概率為
發(fā)生的概率為![]() .
.
故選:![]() .
.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,一幅壁畫的最高點(diǎn)![]() 處離地面
處離地面![]() 米,最低點(diǎn)
米,最低點(diǎn)![]() 處離地面
處離地面![]() 米.正對(duì)壁畫的是一條坡度為
米.正對(duì)壁畫的是一條坡度為![]() 的甬道(坡度指斜坡與水平面所成角
的甬道(坡度指斜坡與水平面所成角![]() 的正切值),若從離斜坡地面
的正切值),若從離斜坡地面![]() 米的
米的![]() 處觀賞它.
處觀賞它.
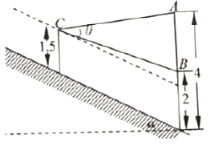
(1)若![]() 對(duì)墻的投影(即過
對(duì)墻的投影(即過![]() 作
作![]() 的垂線垂足為投影)恰在線段
的垂線垂足為投影)恰在線段![]() (包括端點(diǎn))上,求點(diǎn)
(包括端點(diǎn))上,求點(diǎn)![]() 離墻的水平距離的范圍;
離墻的水平距離的范圍;
(2)在(1)的條件下,當(dāng)點(diǎn)![]() 離墻的水平距離為多少時(shí),視角
離墻的水平距離為多少時(shí),視角![]() (
(![]() )最大?
)最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】分配![]() 名工人去
名工人去![]() 個(gè)不同的居民家里檢查管道,要求
個(gè)不同的居民家里檢查管道,要求![]() 名工人都分配出去,并且每名工人只去一個(gè)居民家,且每個(gè)居民家都要有人去檢查,那么分配的方案共有( )
名工人都分配出去,并且每名工人只去一個(gè)居民家,且每個(gè)居民家都要有人去檢查,那么分配的方案共有( )
A.![]() 種B.
種B.![]() 種C.
種C.![]() 種D.
種D.![]() 種
種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校開展“我身邊的榜樣”評(píng)選活動(dòng),現(xiàn)對(duì)3名候選人甲、乙、丙進(jìn)行不記名投票,投票要求詳見選票.這3名候選人的得票數(shù)(不考慮是否有效)分別為總票數(shù)的88%,75%,46%,則本次投票的有效率(有效票數(shù)與總票數(shù)的比值)最高可能為百分之________.
“我身邊的榜樣”評(píng)選選票 | ||
候選人 | 符號(hào) | 注: 1.同意畫“○”,不同意畫“×”. 2.每張選票“○”的個(gè)數(shù)不超過2時(shí)才為有效票. |
甲 | ||
乙 | ||
丙 | ||
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于非負(fù)整數(shù)集合![]() (非空),若對(duì)任意
(非空),若對(duì)任意![]() ,或者
,或者![]() ,或者
,或者![]() ,則稱
,則稱![]() 為一個(gè)好集合.以下記
為一個(gè)好集合.以下記![]() 為
為![]() 的元素個(gè)數(shù).
的元素個(gè)數(shù).
(1)給出所有的元素均小于![]() 的好集合.(給出結(jié)論即可)
的好集合.(給出結(jié)論即可)
(2)求出所有滿足![]() 的好集合.(同時(shí)說明理由)
的好集合.(同時(shí)說明理由)
(3)若好集合![]() 滿足
滿足![]() ,求證:
,求證:![]() 中存在元素
中存在元素![]() ,使得
,使得![]() 中所有元素均為
中所有元素均為![]() 的整數(shù)倍.
的整數(shù)倍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為菱形,PA⊥底面ABCD,∠BAD=60°,AB=PA=4,E是PA的中點(diǎn),AC,BD交于點(diǎn)O.
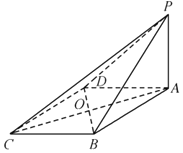
(1)求證:OE∥平面PBC;
(2)求三棱錐E﹣PBD的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 在
在![]() 上的最小值;
上的最小值;
(2)若直線![]() 是函數(shù)
是函數(shù)![]() 的切線方程,求實(shí)數(shù)
的切線方程,求實(shí)數(shù)![]() 的值;
的值;
(3)若![]() ,證明:對(duì)任意實(shí)數(shù)
,證明:對(duì)任意實(shí)數(shù)![]() ,
,![]() 恒成立.
恒成立.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com