
【題目】數列![]() 滿足:
滿足:![]()
(1)求![]() 的值;
的值;
(2)求證:數列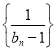 是等差數列,并求數列
是等差數列,并求數列![]() 的通項公式;
的通項公式;
(3)設![]() 假設
假設![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)證明見詳解,
;(2)證明見詳解,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據遞推公式,進行賦值即可求得;
(2)根據等差數列的定義,用其后一項減去前一項,證明其為常數即可;
(3)先根據![]() 利用裂項求和求得
利用裂項求和求得![]() ,再將恒成立問題轉化為二次函數恒成立問題即可.
,再將恒成立問題轉化為二次函數恒成立問題即可.
(1)因為![]()
故可得![]()
因為![]() ,根據
,根據![]() ,可解的
,可解的![]() ;
;
由![]() ,可得
,可得![]()
則![]() ,
,
綜上:![]() ,
,![]() ,
,![]() .
.
(2)證明:由(1)知:![]()
故![]() ,
,
故數列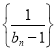 是首項為-4,公差為-1的等差數列,即證.
是首項為-4,公差為-1的等差數列,即證.
故![]() ,解得
,解得![]() .
.
(3)由(2)知![]() ,因為
,因為![]() ,
,
故可得![]()
故![]()
![]()
![]()
![]()
故![]() ,又
,又![]()
故![]() 恒成立,等價于
恒成立,等價于![]() 恒成立,即
恒成立,即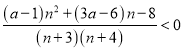 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
令![]() ,
,![]() .
.
當![]() 時,
時,![]() 恒成立,滿足題意;
恒成立,滿足題意;
當![]() 時,由二次函數的性質可知,顯然不成立;
時,由二次函數的性質可知,顯然不成立;
當![]() 時,對稱軸
時,對稱軸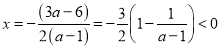
故![]() 在
在![]() 單調遞減,要滿足題意,只需
單調遞減,要滿足題意,只需![]() 即可,即
即可,即![]() ,解得
,解得![]() ,
,
又因為![]() ,故
,故![]() .
.
綜上當![]() 時,
時,![]() 恒成立.
恒成立.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且橢圓上一點與橢圓的兩個焦點構成的三角形周長為
,且橢圓上一點與橢圓的兩個焦點構成的三角形周長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且以
兩點,且以![]() 為直徑的圓過橢圓的右頂點
為直徑的圓過橢圓的右頂點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代中的“禮、樂、射、御、書、數”合稱“六藝”.“禮”,主要指德育;“樂”,主要指美育;“射”和“御”,就是體育和勞動;“書”,指各種歷史文化知識;“數”,指數學.某校國學社團開展“六藝”課程講座活動,每藝安排一節,連排六節,一天課程講座排課有如下要求:“數”必須排在第三節,且“射”和“御”兩門課程相鄰排課,則“六藝”課程講座不同的排課順序共有( )
A.12種B.24種C.36種D.48種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁、戊和己6人圍坐在一張正六邊形的小桌前,每邊各坐一人.已知:①甲與乙正面相對;②丙與丁不相鄰,也不正面相對.若己與乙不相鄰,則以下選項正確的是( )
A.若甲與戊相鄰,則丁與己正面相對B.甲與丁相鄰
C.戊與己相鄰D.若丙與戊不相鄰,則丙與己相鄰
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() .(
.(![]() 且
且![]() )
)
(1)分別判斷當![]() 及
及![]() 時函數的奇偶性;
時函數的奇偶性;
(2)在![]() 且
且![]() 的條件下,將(1)的結論加以推廣,使命題(1)成為推廣后命題的特例,并對推廣的結論加以證明.
的條件下,將(1)的結論加以推廣,使命題(1)成為推廣后命題的特例,并對推廣的結論加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為推動文明城市創建,提升城市整體形象,2018年12月30日鹽城市人民政府出臺了《鹽城市停車管理辦法》,2019年3月1日起施行.這項工作有利于市民養成良好的停車習慣,幫助他們樹立綠色出行的意識,受到了廣大市民的一致好評.現從某單位隨機抽取80名職工,統計了他們一周內路邊停車的時間t(單位:小時),整理得到數據分組及頻率分布直方圖如下:


(1)從該單位隨機選取一名職工,試估計這名職工一周內路邊停車的時間少于8小時的概率;
(2)求頻率分布直方圖中a,b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com