
【題目】已知函數(shù)![]()
![]() (
(![]() 為自然對數(shù)的底數(shù))
為自然對數(shù)的底數(shù))
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當![]() 且
且![]() 時,
時,![]() 在
在![]() 上為減函數(shù),求實數(shù)
上為減函數(shù),求實數(shù)![]() 的最小值.
的最小值.
【答案】(1)當![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上單調(diào)遞增;當
上單調(diào)遞增;當![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;(2)
上單調(diào)遞減;(2)![]() 。
。
【解析】
(Ⅰ)求出函數(shù)g(x)的定義域,函數(shù)的導數(shù)![]() =ex-2﹣a,分a≤0和a>0兩種情況,分別討論函數(shù)的單調(diào)性即可.(Ⅱ)
=ex-2﹣a,分a≤0和a>0兩種情況,分別討論函數(shù)的單調(diào)性即可.(Ⅱ)![]()
![]() 在x∈(1,+∞)上為減函數(shù),轉(zhuǎn)化f'(x)=
在x∈(1,+∞)上為減函數(shù),轉(zhuǎn)化f'(x)=![]()
![]() 0在x∈(1,+∞)恒成立,利用二次函數(shù)
0在x∈(1,+∞)恒成立,利用二次函數(shù)
在對稱軸處取得最值小于等于0推出結(jié)果即可.
(1)![]()
當![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當![]() 時,由
時,由![]() ,得
,得![]() .
.
若![]() ,則
,則![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
若![]() ,則
,則![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞減
上單調(diào)遞減
(2)當![]() 且
且![]() 時,
時,![]()
![]() ,
,
因![]() 在
在![]() 上為減函數(shù),故
上為減函數(shù),故![]() 在
在![]() 上恒成立.
上恒成立.
所以當![]() 時
時![]()
又![]()
![]() ,
,
故當![]() 時,即
時,即![]() 時,
時,![]()
所以![]() ,于是
,于是![]() ,
,
故![]() 的最小值為
的最小值為![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).M是曲線
為參數(shù)).M是曲線![]() 上的動點,將線段OM繞O點順時針旋轉(zhuǎn)
上的動點,將線段OM繞O點順時針旋轉(zhuǎn)![]() 得到線段ON,設點N的軌跡為曲線
得到線段ON,設點N的軌跡為曲線![]() .以坐標原點O為極點,
.以坐標原點O為極點,![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)在(1)的條件下,若射線![]() 與曲線
與曲線![]() 分別交于A, B兩點(除極點外),且有定點
分別交于A, B兩點(除極點外),且有定點![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知a∈R,函數(shù)f(x)=x2﹣2ax+5.
(1)若a>1,且函數(shù)f(x)的定義域和值域均為[1,a],求實數(shù)a的值;
(2)若不等式x|f(x)﹣x2|![]() 1對x∈[
1對x∈[![]() ,
,![]() ]恒成立,求實數(shù)a的取值范圍.
]恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在某次水下考古活動中,需要潛水員潛入水深為30米的水底進行作業(yè).其用氧量包含3個方面:①下潛時,平均速度為![]() (米/單位時間),單位時間內(nèi)用氧量為
(米/單位時間),單位時間內(nèi)用氧量為![]() (
(![]() 為正常數(shù));②在水底作業(yè)需5個單位時間,每個單位時間用氧量為0.4;③返回水面時,平均速度為
為正常數(shù));②在水底作業(yè)需5個單位時間,每個單位時間用氧量為0.4;③返回水面時,平均速度為![]() (米/單位時間), 單位時間用氧量為0.2.記該潛水員在此次考古活動中,總用氧量為
(米/單位時間), 單位時間用氧量為0.2.記該潛水員在此次考古活動中,總用氧量為![]() .
.
(1)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)設0<![]() ≤5,試確定下潛速度
≤5,試確定下潛速度![]() ,使總的用氧量最少.
,使總的用氧量最少.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在△ABC中,AC=BC=![]() AB,四邊形ABED是正方形,平面ABED⊥底面ABC,G,F分別是EC,BD的中點.
AB,四邊形ABED是正方形,平面ABED⊥底面ABC,G,F分別是EC,BD的中點.

(1)求證:GF∥平面ABC;
(2)求證:平面DAC⊥平面EBC.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在5月6日返校體檢中,學號為![]() (
(![]() )的五位同學的體重增加量
)的五位同學的體重增加量![]() 是集合
是集合![]() 中的元素,并滿足
中的元素,并滿足![]() ,則這五位同學的體重增加量所有可能的情況有________種
,則這五位同學的體重增加量所有可能的情況有________種
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】圖是一幾何體的平面展開圖,其中四邊形ABCD為正方形,E,F,G,H分別為![]() ,
,![]() ,
,![]() ,
,![]() 的中點,在此幾何體中,給出下面五個結(jié)論:①平面
的中點,在此幾何體中,給出下面五個結(jié)論:①平面![]() 平面ABCD;②
平面ABCD;②![]() 平面BDG;③
平面BDG;③![]() 平面PBC;④
平面PBC;④![]() 平面BDG;⑤
平面BDG;⑤![]() 平面BDG.
平面BDG.
其中正確結(jié)論的序號是________.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】數(shù)列![]() 滿足:
滿足:![]()
(1)求![]() 的值;
的值;
(2)求證:數(shù)列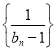 是等差數(shù)列,并求數(shù)列
是等差數(shù)列,并求數(shù)列![]() 的通項公式;
的通項公式;
(3)設![]() 假設
假設![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com