
���}Ŀ����D���������F![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ��
�� ![]() ��
��![]() ��
��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
��1������ֱ��(xi��n)![]() ��
��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��2���c(di��n)![]() �ھ�(xi��n)��
�ھ�(xi��n)��![]() ������
������![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() ����
����![]() ��ֵ��
��ֵ��

���𰸡���1��![]() ��2��
��2��![]() ��
��
��������
ԇ�}��������1�����ÿ��g������(xi��n)��(xi��n)�ǣ��ȸ���(j��)�}��_�����gֱ������(bi��o)ϵ���O(sh��)�����c(di��n)����(bi��o)����ʾֱ��(xi��n)��������������������(sh��)���e�������A������ֵ��������(j��)��(xi��n)��(xi��n)���c�����A���P(gu��n)ϵ�þ�(xi��n)��(xi��n)������ֵ��2�����ÿ��g������(xi��n)��ǣ��ȸ���(j��)�}��_�����gֱ������(bi��o)ϵ���O(sh��)�����c(di��n)����(bi��o)������(j��)���̽M����ķ�����������������(sh��)���e�������A������ֵ��������(j��)��(xi��n)����c�����A�ǻ����P(gu��n)ϵ�е����P(gu��n)ϵ�����![]() ��ֵ��
��ֵ��
ԇ�}��������1��
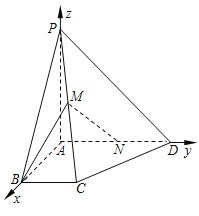
��?y��n)?/span>![]() ƽ��
ƽ��![]() ����
����![]() ƽ��
ƽ��![]() ��
��
����![]() ��
��![]() ��
��
����?y��n)?/span>![]() ������
������![]() �Ƀɻ��ഹֱ��
�Ƀɻ��ഹֱ��
�քe��![]() ��
��![]() �S�������gֱ������(bi��o)ϵ��
�S�������gֱ������(bi��o)ϵ��
�t��![]() ��
��![]() �ɵ�
�ɵ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
����?y��n)?/span>![]() ��
��![]() �����c(di��n)������
�����c(di��n)������![]() ��
��
����![]() ��
��![]() ����������2��
����������2��
����![]()
![]() ��
��
��������ֱ��(xi��n)![]() ��
��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() ����������������������5��
����������������������5��
��2����?y��n)?/span>![]() ������
������![]()
![]() ���t
���t![]() ��
��
![]() ��
��![]() ��
��
�O(sh��)ƽ��![]() �ķ�������
�ķ�������![]() ��
��
�t ��
��![]() ��
��![]() �����
�����![]() ��
��![]() ��
��
����![]() ��ƽ��
��ƽ��![]() ��һ��(g��)������������������������������7��
��һ��(g��)������������������������������7��
��?y��n)�ֱ��(xi��n)![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() ��
��
����![]() ��
��
���![]() ��
��
����![]() ��ֵ��
��ֵ��![]() ������������������������������������������������10��
������������������������������������������������10��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() ���x���ʞ�
���x���ʞ�![]() ����ԭ�c(di��n)
����ԭ�c(di��n)![]() ��A�ģ��E�A
��A�ģ��E�A![]() ���L(zh��ng)���S��돽�ĈA�cֱ��(xi��n)
���L(zh��ng)���S��돽�ĈA�cֱ��(xi��n)![]() ����.
����.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����֪�c(di��n)![]() ��
��![]() ���(d��ng)ֱ��(xi��n)
���(d��ng)ֱ��(xi��n)![]() �c�E�A
�c�E�A![]() �ăɂ�(g��)���c(di��n)����(w��n)����
�ăɂ�(g��)���c(di��n)����(w��n)����![]() �S���Ƿ�����c(di��n)
�S���Ƿ�����c(di��n)![]() ��ʹ
��ʹ![]() �鶨ֵ�������ڣ�ԇ����c(di��n)
�鶨ֵ�������ڣ�ԇ����c(di��n)![]() ������(bi��o)�Ͷ�ֵ���������ڣ�Ո(q��ng)�f(shu��)������.
������(bi��o)�Ͷ�ֵ���������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() �鳣��(sh��)������(sh��)
�鳣��(sh��)������(sh��)![]() ��
��
��1����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ����Сֵ��
����Сֵ��
��2����![]() �Ѓɂ�(g��)�Oֵ�c(di��n)
�Ѓɂ�(g��)�Oֵ�c(di��n)![]() ��
��![]() ��
��![]() ����
����
����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�����C��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ���x���ʞ�
���x���ʞ�![]() ���c(di��n)
���c(di��n)![]() ������(bi��o)ԭ�c(di��n)�����E�A
������(bi��o)ԭ�c(di��n)�����E�A![]() �c����(xi��n)
�c����(xi��n)![]() �Ľ��c(di��n)�քe��
�Ľ��c(di��n)�քe��![]() ��
��![]() ��
��![]() �ϣ�����
�ϣ�����![]() ���c(di��n)�M(m��n)��
���c(di��n)�M(m��n)��![]() ��
��
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���^(gu��)�E�A![]() �Ϯ�������c(di��n)����һ�c(di��n)
�Ϯ�������c(di��n)����һ�c(di��n)![]() ����
����![]() �ăɗl�о�(xi��n)�����c(di��n)�քe��
�ăɗl�о�(xi��n)�����c(di��n)�քe��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() ��
��![]() �S��
�S��![]() �S�ϵĽؾ�քe��
�S�ϵĽؾ�քe��![]() ���C����
���C����![]() �鶨ֵ��
�鶨ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���タ(xi��n)![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ��
��![]() �Ϯ���ԭ�c(di��n)������һ�c(di��n)���^(gu��)�c(di��n)
�Ϯ���ԭ�c(di��n)������һ�c(di��n)���^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() ��
��![]() ����һ�c(di��n)
����һ�c(di��n)![]() ����
����![]() �S�������S���c(di��n)
�S�������S���c(di��n)![]() ������
������![]() ����(d��ng)�c(di��n)
����(d��ng)�c(di��n)![]() �M����(bi��o)��
�M����(bi��o)��![]() �r(sh��)��
�r(sh��)��![]() ������������
������������
��1����![]() �ķ��̣�
�ķ��̣�
��2����ֱ��(xi��n)![]() ����
����![]() ��
�� ![]() ����ֻ��һ��(g��)�����c(di��n)
����ֻ��һ��(g��)�����c(di��n)![]() ��
��
���C��ֱ��(xi��n)![]() �^(gu��)���c(di��n)����������c(di��n)����(bi��o)��
�^(gu��)���c(di��n)����������c(di��n)����(bi��o)��
��![]() ����e�Ƿ������Сֵ�������ڣ�Ո(q��ng)�����Сֵ���������ڣ�Ո(q��ng)�f(shu��)��������
����e�Ƿ������Сֵ�������ڣ�Ո(q��ng)�����Сֵ���������ڣ�Ո(q��ng)�f(shu��)��������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ![]() �У���֪�A
�У���֪�A![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ��
��
��1����ֱ��(xi��n)![]() ƽ����
ƽ����![]() ���c�A
���c�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �ķ��̣�
�ķ��̣�
��2���ڈA![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ��
��ʹ��![]() �������ڣ����c(di��n)
�������ڣ����c(di��n)![]() �Ă�(g��)��(sh��)���������ڣ��f(shu��)��������
�Ă�(g��)��(sh��)���������ڣ��f(shu��)��������

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij�߿Ƽ���I(y��)���a(ch��n)�a(ch��n)Ʒ![]() �ͮa(ch��n)Ʒ
�ͮa(ch��n)Ʒ![]() ��Ҫ�ס��҃ɷN���Ͳ��ϣ����a(ch��n)һ���a(ch��n)Ʒ
��Ҫ�ס��҃ɷN���Ͳ��ϣ����a(ch��n)һ���a(ch��n)Ʒ![]() ��Ҫ�ײ���1.5
��Ҫ�ײ���1.5![]() ���Ҳ���1
���Ҳ���1![]() ����5��(g��)���r(sh��)�����a(ch��n)һ���a(ch��n)Ʒ��Ҫ�ײ���0.5
����5��(g��)���r(sh��)�����a(ch��n)һ���a(ch��n)Ʒ��Ҫ�ײ���0.5![]() ���Ҳ���0.3
���Ҳ���0.3![]() ����3��(g��)���r(sh��)�����a(ch��n)һ���a(ch��n)Ʒ������(r��n)��2100Ԫ�����a(ch��n)һ���a(ch��n)Ʒ������(r��n)��900Ԫ��ԓ��I(y��)�F(xi��n)�мײ���150
����3��(g��)���r(sh��)�����a(ch��n)һ���a(ch��n)Ʒ������(r��n)��2100Ԫ�����a(ch��n)һ���a(ch��n)Ʒ������(r��n)��900Ԫ��ԓ��I(y��)�F(xi��n)�мײ���150![]() ���Ҳ���90
���Ҳ���90![]() ���t�ڲ����^(gu��)600��(g��)���r(sh��)�ėl���£����a(ch��n)�a(ch��n)Ʒ
���t�ڲ����^(gu��)600��(g��)���r(sh��)�ėl���£����a(ch��n)�a(ch��n)Ʒ![]() ������(r��n)֮�͵����ֵ��_(k��i)___________Ԫ��
������(r��n)֮�͵����ֵ��_(k��i)___________Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������D��ʾ�ĈA�_(t��i)�У�![]() ���µ���A
���µ���A![]() ��ֱ����
��ֱ����![]() ���ϵ���A
���ϵ���A![]() ��ֱ����
��ֱ����![]() �LjA�_(t��i)��һ�lĸ��(xi��n)��
�LjA�_(t��i)��һ�lĸ��(xi��n)��
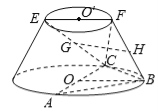
��1����֪![]() ��
��![]() �քe��
�քe��![]() ��
��![]() �����c(di��n)�����C��
�����c(di��n)�����C��![]() ƽ��
ƽ��![]() ��
��
��2����֪![]() ��
��![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
��1����(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2���C������(d��ng)![]() �r(sh��)���P(gu��n)��
�r(sh��)���P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() �������
�������
��3��������(sh��)��(sh��)![]() �M(m��n)��
�M(m��n)��![]() ���C��
���C��![]() ��
��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com