【題目】設直線
與橢圓
相交于
，
兩個不同的點，與
軸相交于點
，
為坐標原點.
（1）證明：
；
（2）若
，求
的面積取得最大值時橢圓的方程.
【答案】（1）
.
（2）
的面積取得最大值時橢圓的方程是
.
【解析】
（1）設直線l的方程為y=k（x+1），將直線的方程代入拋物線的方程，消去x得到關于y的一元二次方程，再結合直線l與橢圓相交于兩個不同的點得到根的判別式大于0，從而解決問題；
（2）設A（x1，y1），B（x2，y2），由（1）得
，由
=3
得y2=
，從而求得△OAB的面積，最后利用基本不等式求得其最大值及取值最大值時的k值，從而△OAB的面積取得最大值時橢圓方程可求．
（1）依題意，直線
顯然不平行于坐標軸，故
可化為
.
將代入
，消去
，
得
，①
由直線與橢圓相交于兩個不同的點，
，整理得.
（2）設
，
.由①，得，
因為
，得
，代入上式，得
.
于是，的面積
，
其中，上式取等號的條件是
，即
.
由，可得
.
將
，
及
，
這兩組值分別代入①，均可解出
.
所以，的面積取得最大值時橢圓的方程是
.
科目：高中數學 來源： 題型：
【題目】設
是一個由
和
構成的
行
列的數表，且中所有數字之和不小于
，所有這樣的數表構成的集合記為
，記
為的第
行各數之和
，
為的第
列各數之和
，
為
、
、
，
、
、
、、
中的最大值.
（1）對如下數表，求的值；
|
|
|
|
|
|
|
|
（2）設數表
，求的最小值；
（3）已知
為正整數，對于所有的
，
，且的任意兩行中最多有
列各數之和為，求的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，底面ABCD為正方形，平面PAD⊥底面ABCD，PD⊥AD，PD=AD，E為棱PC的中點
（I）證明：平面PBC⊥平面PCD；
（II）求直線DE與平面PAC所成角的正弦值；
（III）若F為AD的中點，在棱PB上是否存在點M，使得FM⊥BD？若存在，求
的值，若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某手機生產廠商為迎接5G時代的到來，要生產一款5G手機，在生產之前，該公司對手機屏幕的需求尺寸進行社會調查，共調查了400人，將這400人按對手機屏幕的需求尺寸分為6組，分別是：
，
，
，
，
，
（單位：英寸），得到如下頻率分布直方圖：
其中，屏幕需求尺寸在的一組人數為50人．
（1）求a和b的值；
（2）用分層抽樣的方法在屏幕需求尺寸為和兩組人中抽取6人參加座談，并在6人中選擇2人做代表發言，則這2人來自同一分組的概率是多少？
（3）若以廠家此次調查結果的頻率作為概率，市場隨機調查兩人，這兩人屏幕需求尺寸分別在和的概率是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市為了解游客人數的變化規律，提高旅游服務質量，收集并整理了2014年1月至2016年12月期間月接待游客量（單位：萬人）的數據，繪制了如圖所示的折線圖.根據該折線圖，下列結論錯誤的是（ ）
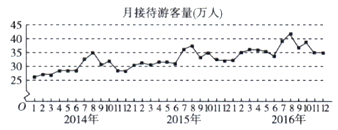
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7，8月
D.各年1月至6月的月接待游客量相對于7月至12月，波動性更小，變化比較平穩
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}中的項按順序可以排成如圖的形式，第一行1項，排a1；第二行2項，從左到右分別排a2，a3；第三行3項，……依此類推，設數列{an}的前n項和為Sn，則滿足Sn＞2019的最小正整數n的值為（）
A. 20B. 21C. 26D. 27
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，長方體ABCD﹣A1B1C1D1中，AB＝BC＝4，BB1＝2
，點E、F、M分別為C1D1，A1D1，B1C1的中點，過點M的平面α與平面DEF平行，且與長方體的面相交，交線圍成一個幾何圖形．
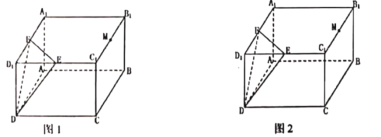
（1）在圖1中，畫出這個幾何圖形，并求這個幾何圖形的面積（不必說明畫法與理由）
（2）在圖2中，求證：D1B⊥平面DEF．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量
(噸)與相應的生產能耗
(噸)標準煤的幾組對照數據
|
|
|
|
|
|
|
|
|
|
(1)請根據上表提供的數據，用最小二乘法求出關于的線性回歸方程
；
(2)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤．試根據(1)求出的線性回歸方程，預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
參考公式：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司將進貨單價為8元一個的商品按10元一個出售，每天可以賣出100個，若這種商品的售價每個上漲1元，則銷售量就減少10個．
（1）求售價為13元時每天的銷售利潤；
（2）求售價定為多少元時，每天的銷售利潤最大，并求最大利潤．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
