
【題目】已知函數![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 與曲線
與曲線![]() 的公切線的方程;
的公切線的方程;
(2)設函數![]() 的兩個極值點為
的兩個極值點為![]() ,求證:關于
,求證:關于![]() 的方程
的方程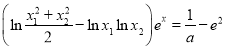 有唯一解.
有唯一解.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】
(1)求兩條曲線的公切線,分別求出各自的切線,然后兩條切線為同一條直線,結合兩個方程求解;
(2)要證明關于![]() 的方程
的方程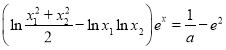 有唯一解,只要證明
有唯一解,只要證明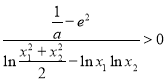 即可,由于當
即可,由于當![]() 時,
時,![]() 單調遞增,不可能有兩個零點,故
單調遞增,不可能有兩個零點,故![]() 不可能有兩個極值點,故
不可能有兩個極值點,故![]() ,利用
,利用![]() 得
得![]() ,又
,又![]()
![]() ,接下來只要證明
,接下來只要證明![]() ,即
,即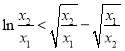 ,令
,令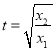 ,則只要證明
,則只要證明![]() 即可,用導數即可證明.
即可,用導數即可證明.
(1)曲線![]() 在切點
在切點![]() 處的切線方程為
處的切線方程為
![]() ,即
,即![]() ,
,
曲線![]() 在切點
在切點![]() 處的切線方程為
處的切線方程為
![]() ,即
,即![]() ,
,
由曲線![]() 與曲線
與曲線![]() 存在公切線,
存在公切線,
得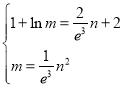 ,得
,得![]() ,即
,即![]() .
.
令![]() ,則
,則![]() ,
,
![]() ,解得
,解得![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,解得
,解得![]() ,∴
,∴![]() 在
在![]() 上單調遞減,
上單調遞減,
又![]() ,∴
,∴![]() ,則
,則![]() ,
,
故公切線方程為![]() .
.
(2)要證明關于![]() 的方程
的方程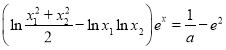 有唯一解,
有唯一解,
只要證明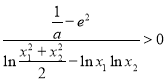 ,
,
先證明:![]() .
.
∵![]() 有兩個極值點,
有兩個極值點,
∴![]() 有兩個不同的零點,
有兩個不同的零點,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() 恒成立,∴
恒成立,∴![]() 單調遞增,
單調遞增,![]() 不可能有兩個零點;
不可能有兩個零點;
當![]() 時,
時,![]() ,則
,則![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,則
,則![]() ,∴
,∴![]() 在
在![]() 上單調遞減,
上單調遞減,
又![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
∴![]() ,得
,得![]() ,∴
,∴![]() .
.
易知![]() ,
,
由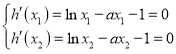 ,得
,得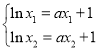 ,
,![]() ,
,
∴![]() .
.
下面再證明:![]() .
.
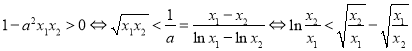 ,
,
令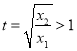 ,則只需證
,則只需證![]() ,
,
令![]() ,
,
則![]() ,
,
∴![]() ,得
,得![]() .
.
∴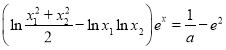 有唯一解.
有唯一解.


 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)函數![]() ,討論
,討論![]() 的單調性;
的單調性;
(2)曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,是否存在這樣的點
,是否存在這樣的點![]() 使得直線
使得直線![]() 與曲線
與曲線![]() 也相切,若存在,判斷滿足條件的點
也相切,若存在,判斷滿足條件的點![]() 的個數,若不存在,請說明理由.
的個數,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘著名數學家阿波羅尼斯與歐幾里得、阿基米德齊名.他發現:“平面內到兩個定點![]() 的距離之比為定值
的距離之比為定值![]() 的點的軌跡是圓”.后來,人們將這個圓以他的名字命名,稱為阿波羅尼斯圓,簡稱阿氏圓在平面直角坐標系
的點的軌跡是圓”.后來,人們將這個圓以他的名字命名,稱為阿波羅尼斯圓,簡稱阿氏圓在平面直角坐標系![]() 中,
中,![]() 點
點![]() .設點
.設點![]() 的軌跡為
的軌跡為![]() ,下列結論正確的是( )
,下列結論正確的是( )
A. ![]() 的方程為
的方程為![]()
B. 在![]() 軸上存在異于
軸上存在異于![]() 的兩定點
的兩定點![]() ,使得
,使得![]()
C. 當![]() 三點不共線時,射線
三點不共線時,射線![]() 是
是![]() 的平分線
的平分線
D. 在![]() 上存在點
上存在點![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一種新的驗血技術可以提高血液檢測效率.現某專業檢測機構提取了![]() 份血液樣本,其中只有1份呈陽性,并設計了如下混合檢測方案:先隨機對其中
份血液樣本,其中只有1份呈陽性,并設計了如下混合檢測方案:先隨機對其中![]() 份血液樣本分別取樣,然后再混合在一起進行檢測,若檢測結果為陰性,則對另外3份血液逐一檢測,直到確定呈陽性的血液為止;若檢測結果呈陽性,測對這
份血液樣本分別取樣,然后再混合在一起進行檢測,若檢測結果為陰性,則對另外3份血液逐一檢測,直到確定呈陽性的血液為止;若檢測結果呈陽性,測對這![]() 份血液再逐一檢測,直到確定呈陽性的血液為止.
份血液再逐一檢測,直到確定呈陽性的血液為止.
(1)若![]() ,求恰好經過3次檢測而確定呈陽性的血液的事件概率;
,求恰好經過3次檢測而確定呈陽性的血液的事件概率;
(2)若![]() ,宜采用以上方案檢測而確定呈陽性的血液所需次數為
,宜采用以上方案檢測而確定呈陽性的血液所需次數為![]() ,
,
①求![]() 的概率分布;
的概率分布;
②求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,已知菱形![]() 的對角線
的對角線![]() 交于點
交于點![]() ,點
,點![]() 為線段
為線段![]() 的中點,
的中點,![]() ,
,![]() ,將三角形
,將三角形![]() 沿線段
沿線段![]() 折起到
折起到![]() 的位置,
的位置,![]() ,如圖2所示.
,如圖2所示.

(Ⅰ)證明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為生產一種精密管件研發了一臺生產該精密管件的車床,該精密管件有內外兩個口徑,監管部門規定“口徑誤差”的計算方式為:管件內外兩個口徑實際長分別為![]() ,標準長分別為
,標準長分別為![]() 則“口徑誤差”為
則“口徑誤差”為![]() 只要“口徑誤差”不超過
只要“口徑誤差”不超過![]() 就認為合格,已知這臺車床分晝夜兩個獨立批次生產.工廠質檢部在兩個批次生產的產品中分別隨機抽取40件作為樣本,經檢測其中晝批次的40個樣本中有4個不合格品,夜批次的40個樣本中有10個不合格品.
就認為合格,已知這臺車床分晝夜兩個獨立批次生產.工廠質檢部在兩個批次生產的產品中分別隨機抽取40件作為樣本,經檢測其中晝批次的40個樣本中有4個不合格品,夜批次的40個樣本中有10個不合格品.
(Ⅰ)以上述樣本的頻率作為概率,在晝夜兩個批次中分別抽取2件產品,求其中恰有1件不合格產品的概率;
(Ⅱ)若每批次各生產1000件,已知每件產品的成本為5元,每件合格品的利潤為10元;若對產品檢驗,則每件產品的檢驗費用為2.5元;若有不合格品進入用戶手中,則工廠要對用戶賠償,這時生產的每件不合格品工廠要損失25元.以上述樣本的頻率作為概率,以總利潤的期望值為決策依據,分析是否要對每個批次的所有產品作檢測?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,圓
為坐標原點,圓![]() :
:![]() ,定點
,定點![]() ,點
,點![]() 是圓
是圓![]() 上一動點,線段
上一動點,線段![]() 的垂直平分線交圓
的垂直平分線交圓![]() 的半徑
的半徑![]() 于點
于點![]() ,點
,點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)不垂直于![]() 軸且不過
軸且不過![]() 點的直線
點的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,若直線
兩點,若直線![]() 、
、![]() 的斜率之和為0,則動直線
的斜率之和為0,則動直線![]() 是否一定經過一定點?若過一定點,則求出該定點的坐標;若不過定點,請說明理由.
是否一定經過一定點?若過一定點,則求出該定點的坐標;若不過定點,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com