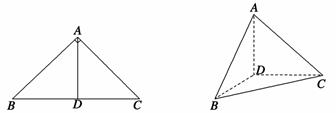
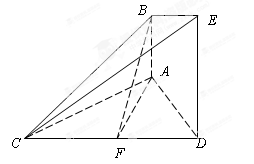
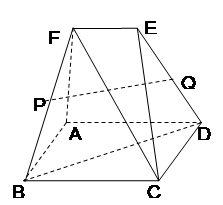如圖,在
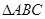
中,
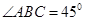
,
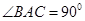
,
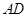
是
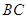
上的高,沿
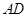
把
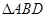
折起,使
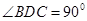
.
(Ⅰ)證明:平面
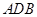
⊥平面
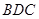
;
(Ⅱ)若
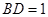
,求三棱錐
的表面積.
(Ⅰ)證明詳見解析;(Ⅱ)
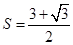
.
試題分析:(Ⅰ)先證線面垂直
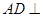
平面
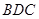
,再證明面面垂直平面
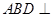
平面
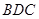
;(Ⅱ)由第一問可知
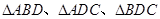
都是直角三角形,可以求出
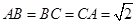
,所以
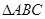
是等邊三角形,分別求出四個三角形的面積.
試題解析:(Ⅰ)因為折起前
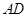
是
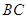
邊上的高.
所以當
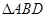
折起后,
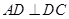
,
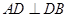
, 3分
又
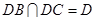
,所以
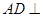
平面
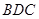
,因為
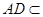
平面
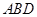
,
所以平面
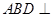
平面
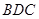
. 6分
(Ⅱ)由(1)知,
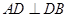
,
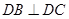
,
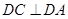
,
因為
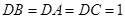
,
所以
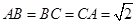
, 9分
從而
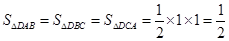
,
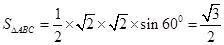
,
所以三棱錐
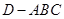
的表面積
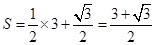
. 12分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
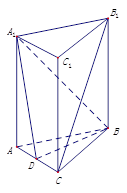
如圖,在直三棱柱
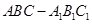
中,
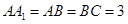
,
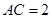
,
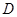
是
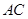
的中點.
(Ⅰ)求證:
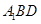
平面
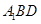
;
(Ⅱ)求二面角
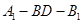
的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在長方體
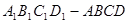
中,
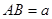
,
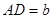
,
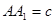
,
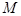
是線段
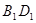
的中點.
(Ⅰ)求證:
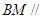
平面
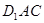
;
(Ⅱ)求平面
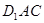
把長方體
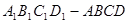
分成的兩部分的體積比.
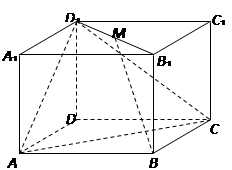
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
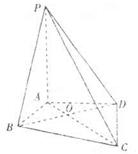
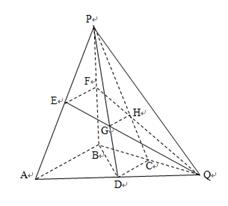
如圖,在四棱錐P-ABCD中,PA丄平面ABCD,
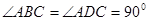
,
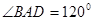
,AD=AB=1,AC和BD交于O點.
(I)求證:平面PBD丄平面PAC.
(II)當點A在平面PBD內(nèi)的射影G恰好是ΔPBD的重心時,求二面角B-PD-A的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖, 在三棱錐
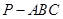
中,
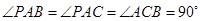
.

(1)求證:平面
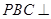
平面
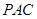
;
(2)若
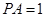
,
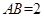
,當三棱錐
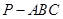
的體積最大時,求
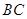
的長.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,多面體
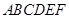
中,四邊形
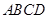
是邊長為
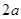
的正方形,平面
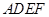
垂直于平面
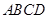
,且
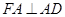
,
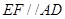
,
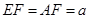
.
(Ⅰ)求證:
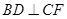
;
(Ⅱ)若
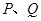
分別為棱
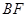
和
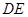
的中點,求證:
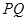
∥平面
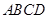
;
(Ⅲ)求多面體
的體積.
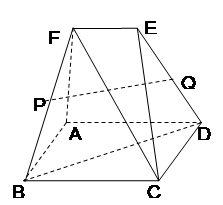
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖所示,在三棱錐
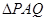
中,
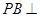
平面
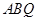
,
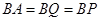
,
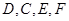
分別是
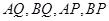
的中點,
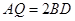
,
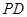
與
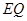
交于
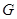
,
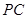
與
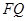
交于點
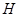
,連接
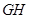
。
(Ⅰ)求證:
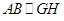
;
(Ⅱ)求二面角

的余弦值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,已知
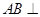
平面
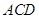
,
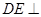
平面
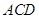
,△
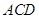
為等邊三角形,
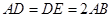
,
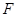
為
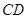
的中點.
(1)求證:
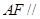
平面
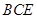
;
(2)求證:平面
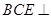
平面
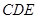
;
(3)求直線
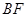
和平面
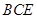
所成角的正弦值.
查看答案和解析>>

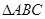 中,
中,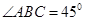 ,
,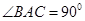 ,
,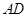 是
是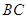 上的高,沿
上的高,沿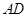 把
把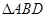 折起,使
折起,使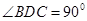 .
.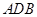 ⊥平面
⊥平面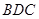 ;
;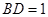 ,求三棱錐
,求三棱錐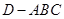 的表面積.
的表面積.
 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案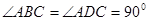 ,
,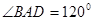 ,AD=AB=1,AC和BD交于O點.
,AD=AB=1,AC和BD交于O點.
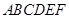 中,四邊形
中,四邊形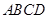 是邊長為
是邊長為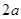 的正方形,平面
的正方形,平面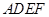 垂直于平面
垂直于平面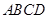 ,且
,且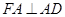 ,
,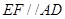 ,
,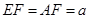 .
.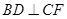 ;
;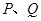 分別為棱
分別為棱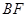 和
和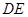 的中點,求證:
的中點,求證: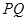 ∥平面
∥平面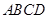 ;
;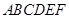 的體積.
的體積.