
【題目】已知點![]() 、
、![]() 為雙曲線
為雙曲線![]()
![]() 的左、右焦點,過
的左、右焦點,過![]() 作垂直于
作垂直于![]() 軸的直線,在
軸的直線,在![]() 軸上方交雙曲線
軸上方交雙曲線![]() 于點
于點![]() ,且
,且![]() ,圓
,圓![]() 的方程是
的方程是![]() .
.
(1)求雙曲線![]() 的方程;
的方程;
(2)過雙曲線![]() 上任意一點
上任意一點![]() 作該雙曲線兩條漸近線的垂線,垂足分別為
作該雙曲線兩條漸近線的垂線,垂足分別為![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)過圓![]() 上任意一點
上任意一點![]() 作圓
作圓![]() 的切線
的切線![]() 交雙曲線
交雙曲線![]() 于
于![]() 、
、![]() 兩點,
兩點,![]() 中點為
中點為![]() ,求證:
,求證:![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)詳見解析.
;(3)詳見解析.
【解析】
(1)![]() ,根據
,根據![]() 可得
可得![]() ,利用雙曲線的定義可得
,利用雙曲線的定義可得![]() 從而得到雙曲線的方程.
從而得到雙曲線的方程.
(2)設點![]() ,利用漸近線的斜率可以得到
,利用漸近線的斜率可以得到![]() 夾角的余弦為
夾角的余弦為![]() ,利用點在雙曲線上又可得
,利用點在雙曲線上又可得![]() 為定值
為定值![]() ,故可得
,故可得![]() 的值.
的值.
(3)設![]() ,切線
,切線![]() 的方程為:
的方程為:![]() ,證明
,證明![]() 等價于證明
等價于證明![]() ,也就是證明
,也就是證明 ![]() ,聯立切線方程和雙曲線方程,消元后利用韋達定理可以證明
,聯立切線方程和雙曲線方程,消元后利用韋達定理可以證明![]() .
.
(1)設![]() 的坐標分別為
的坐標分別為![]() ,
,![]()
因為點![]() 在雙曲線
在雙曲線![]() 上,所以
上,所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
在![]() 中,
中, ![]() ,
,![]() ,所以
,所以![]() ,
,
由雙曲線的定義可知: ![]() ,
,
故雙曲線![]() 的方程為:
的方程為: ![]() .
.
(2)由條件可知:兩條漸近線分別為![]() ;
;![]() .
.
設雙曲線![]() 上的點
上的點![]() ,
,
設![]() 的傾斜角為
的傾斜角為![]() ,則
,則![]() ,又
,又![]() ,所以
,所以![]() ,
,
故![]() ,
,
所以![]() 的夾角為
的夾角為![]() ,且
,且![]() .
.
點![]() 到兩條漸近線的距離分別為
到兩條漸近線的距離分別為![]() ,
,![]() .
.
因為![]() 在雙曲線
在雙曲線![]() 上,所以
上,所以![]() ,
,
所以![]()
![]()
![]() .
.
(3)由題意,即證: ![]() ,設
,設![]() ,
,
切線![]() 的方程為:
的方程為: ![]() .
.
![]() 時,切線
時,切線![]() 的方程代入雙曲線
的方程代入雙曲線![]() 中,化簡得:
中,化簡得:
(![]()
![]() ,
,
所以![]() ,
,![]() .
.
又![]()
![]()
![]() ,
,
所以![]()
![]()
![]() .
.
![]() 時,易知上述結論也成立.所以
時,易知上述結論也成立.所以![]() .
.
綜上, ![]() ,所以
,所以![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,三棱錐P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一點,且CD⊥平面PAB.
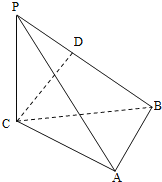
(1)求證:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知雙曲線的中心在原點,焦點在x軸上,實軸長為4,漸近線方程為![]() .求雙曲線的標準方程;
.求雙曲線的標準方程;
(2)過(1)中雙曲線上一點P的直線分別交兩條漸近于![]() 兩點,且P是線段AB的中點,求證:
兩點,且P是線段AB的中點,求證:![]() 為常數;
為常數;
(3)我們知道函數![]() 的圖象是由雙曲線
的圖象是由雙曲線![]() 的圖象逆時針旋轉45°得到的,函數
的圖象逆時針旋轉45°得到的,函數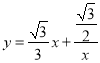 的圖象也是雙曲線,請嘗試寫出曲線
的圖象也是雙曲線,請嘗試寫出曲線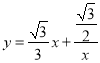 的性質(不必證明).
的性質(不必證明).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】采用系統抽樣方法從1000人中抽取50人做問卷調查,為此將他們隨機編號1,, ,1000,適當分組后在第一組采用簡單隨機抽樣的方法抽到的號碼為8,抽到的50人中,編號落入區間![]() 的人做問卷A,編號落入區間
的人做問卷A,編號落入區間![]() 的人做問卷B,其余的人做問卷C,則抽到的人中,做問卷C的人數為( )
的人做問卷B,其余的人做問卷C,則抽到的人中,做問卷C的人數為( )
A. 12 B. 13 C. 14 D. 15
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在股票市場上,投資者常根據股價![]() 每股的價格
每股的價格![]() 走勢圖來操作,股民老張在研究某只股票時,發現其在平面直角坐標系內的走勢圖有如下特點:每日股價
走勢圖來操作,股民老張在研究某只股票時,發現其在平面直角坐標系內的走勢圖有如下特點:每日股價![]() 元
元![]() 與時間
與時間![]() 天
天![]() 的關系在ABC段可近似地用函數
的關系在ABC段可近似地用函數![]() 的圖象從最高點A到最低點C的一段來描述
的圖象從最高點A到最低點C的一段來描述![]() 如圖
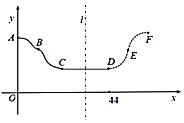
如圖![]() ,并且從C點到今天的D點在底部橫盤整理,今天也出現了明顯的底部結束信號.老張預測這只股票未來一段時間的走勢圖會如圖中虛線DEF段所示,且DEF段與ABC段關于直線l:
,并且從C點到今天的D點在底部橫盤整理,今天也出現了明顯的底部結束信號.老張預測這只股票未來一段時間的走勢圖會如圖中虛線DEF段所示,且DEF段與ABC段關于直線l:![]() 對稱,點B,D的坐標分別是
對稱,點B,D的坐標分別是![]() .
.
![]() 請你幫老張確定a,
請你幫老張確定a,![]() ,
,![]() 的值,并寫出ABC段的函數解析式;
的值,并寫出ABC段的函數解析式;
![]() 如果老張預測準確,且今天買入該只股票,那么買入多少天后股價至少是買入價的兩倍?
如果老張預測準確,且今天買入該只股票,那么買入多少天后股價至少是買入價的兩倍?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小組有7個同學,其中4個同學從來沒有參加過天文研究性學習活動,3個同學曾經參加過天文研究性學習活動.
(1)現從該小組中隨機選2個同學參加天文研究性學習活動,求恰好選到1個曾經參加過天文研究性學習活動的同學的概率;
(2)若從該小組隨機選2個同學參加天文研究性學習活動,則活動結束后,該小組有參加過天文研究性學習活動的同學個數![]() 是一個隨機變量,求隨機變量
是一個隨機變量,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面幾種推理是類比推理的( )
A. 兩條直線平行,同旁內角互補,如果![]() 和
和![]() 是兩條平行直線的同旁內角,則
是兩條平行直線的同旁內角,則![]()
B. 由平面三角形的性質,推測空間四邊形的性質
C. 某校高二級有20個班,1班有51位團員,2班有53位團員,3班有52位團員,由此可以推測各班都超過50位團員.
D. 一切偶數都能被2整除,![]() 是偶數,所以
是偶數,所以![]() 能被2整除.
能被2整除.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com