
【題目】連續投骰子兩次得到的點數分別為m,n,作向量![]() (m,n),則
(m,n),則![]() 與
與![]() (1,﹣1)的夾角成為直角三角形內角的概率是_____.
(1,﹣1)的夾角成為直角三角形內角的概率是_____.
 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 是邊長為2的菱形,且
是邊長為2的菱形,且![]() .四邊形
.四邊形![]() 是平行四邊形,且
是平行四邊形,且![]() .點
.點![]() ,
,![]() 在平面
在平面![]() 內的射影為
內的射影為![]() ,
,![]() ,且
,且![]() 在
在![]() 上,四棱錐
上,四棱錐![]() 的體積為2.
的體積為2.
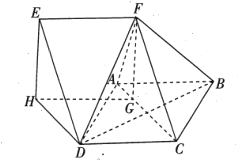
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ?如果存在,是確定點
?如果存在,是確定點![]() 的位置,如果不存在,請說明理由.
的位置,如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據歷史記載,美日在中途島(Midway)海戰前,美方截獲了日方密碼電報,據美方已破譯的密碼得知,日方將向某島進行軍事活動,但關鍵含有地點的部分卻被日方換成了另一種密碼.經專家研究,估計是一種密匙密碼,且密匙為3位.所謂密匙密碼是指:將一段英文字母的明文(未加密前原文)經過對某一組數字(即密匙)的變換,改變成了另一組英文字母成為密文(加密后的文字)例如:明文:![]() (不計空格,不計大小寫)在密匙為:1 9 2的條件下,變換過程如下圖所示:
(不計空格,不計大小寫)在密匙為:1 9 2的條件下,變換過程如下圖所示:
s | t | u | d | e | n | t |
1 | 9 | 2 | 1 | 9 | 2 | 1 |
t | c | w | e | n | p | u |
則密文為:![]() ,試根據上面信息回答下面問題:
,試根據上面信息回答下面問題:
(1)在密匙為111的條件下,填寫下表,并寫出密文;
s | t | u | d | e | n | t |
密文____________________.
(2)若![]()
![]() 請填寫下表,并寫出密匙;
請填寫下表,并寫出密匙;
s | t | u | d | e | n | t |
密匙為_____________.
(3)若下面即是那段包含地點(Midway)的破譯不出的密文:![]() ,且此段密文也是3位密匙加密,試填寫下表,寫出密匙,并將此段密文翻譯成明文.(不必證明,寫出明文即可)
,且此段密文也是3位密匙加密,試填寫下表,寫出密匙,并將此段密文翻譯成明文.(不必證明,寫出明文即可)
c | w | b | c | f | s | o | l | l | y | d | g |
密匙為___________,明文為_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
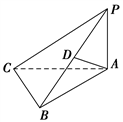
【題目】如圖所示,在三棱錐P–ABC中,PA⊥平面ABC,D是棱PB的中點,已知PA=BC=2,AB=4,CB⊥AB,則異面直線PC,AD所成角的余弦值為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2017年1月至2019年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論錯誤的是( )

A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位數為30萬人
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①在直角梯形ABCP中,![]() ,
,![]() ,
,![]() ,
,![]() ,E,F,G分別是線段PC,PD,BC的中點,現將
,E,F,G分別是線段PC,PD,BC的中點,現將![]() 折起,使平面
折起,使平面![]() 平面ABCD如圖②.
平面ABCD如圖②.
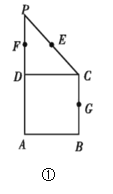
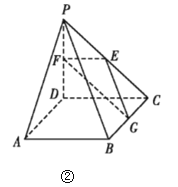
(1)求證:![]() 平面EFG;
平面EFG;
(2)求二面角G—EF—D的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,某地出土的一種“釘”是由四條線段組成,其結構能使它任意拋至水平面后,總有一端所在的直線豎直向上,并記組成該“釘”的四條線段的公共點為O,釘尖為![]() .
.
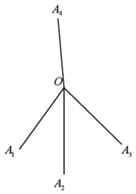
⑴設![]() ,當
,當![]() ,
,![]() ,
,![]() 在同一水平面內時,求
在同一水平面內時,求![]() 與平面
與平面![]() 所成角的大小
所成角的大小![]() 結果用反三角函數值表示
結果用反三角函數值表示![]() .
.
⑵若該“釘”的三個釘尖所確定的三角形的面積為![]() ,要用某種線型材料復制100枚這種“釘”
,要用某種線型材料復制100枚這種“釘”![]() 損耗忽略不計
損耗忽略不計![]() ,共需要該種材料多少米?
,共需要該種材料多少米?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年國際籃聯籃球世界杯,將于2019年在的北京、廣州、南京、上海、武漢、深圳、佛山、東莞八座城市舉行.為了宣傳世界杯,某大學從全校學生中隨機抽取了![]() 名學生,對是否收看籃球世界杯賽事的情況進行了問卷調查,統計數據如下:
名學生,對是否收看籃球世界杯賽事的情況進行了問卷調查,統計數據如下:
會收看 | 不會收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根據上表說明,能否有![]() 的把握認為收看籃球世界杯賽事與性別有關?
的把握認為收看籃球世界杯賽事與性別有關?
(2)現從參與問卷調查且收看籃球世界杯賽事的學生中,采用按性別分層抽樣的方法選取![]() 人參加2019年國際籃聯籃球世界杯賽志愿者宣傳活動.
人參加2019年國際籃聯籃球世界杯賽志愿者宣傳活動.
(i)求男、女學生各選取多少人;
(ii)若從這![]() 人中隨機選取
人中隨機選取![]() 人到校廣播站開展2019年國際籃聯籃球世界杯賽宣傳介紹,求恰好選到
人到校廣播站開展2019年國際籃聯籃球世界杯賽宣傳介紹,求恰好選到![]() 名男生的概率.
名男生的概率.
附: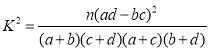 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com