
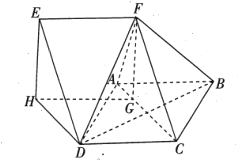
【題目】如圖,四邊形![]() 是邊長為2的菱形,且
是邊長為2的菱形,且![]() .四邊形
.四邊形![]() 是平行四邊形,且
是平行四邊形,且![]() .點
.點![]() ,
,![]() 在平面
在平面![]() 內的射影為
內的射影為![]() ,
,![]() ,且
,且![]() 在
在![]() 上,四棱錐
上,四棱錐![]() 的體積為2.
的體積為2.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ?如果存在,是確定點
?如果存在,是確定點![]() 的位置,如果不存在,請說明理由.
的位置,如果不存在,請說明理由.
【答案】(1)見解析;(2)![]() 是靠近點
是靠近點![]() 的四等分點,理由見解析
的四等分點,理由見解析
【解析】
(1)先由線面垂直的判定定理,證明![]() 平面
平面![]() ,再由面面垂直的判定定理,即可證明結論成立;
,再由面面垂直的判定定理,即可證明結論成立;
(2)先由四棱錐的體積求出![]() ,得出
,得出![]() ,即點
,即點![]() 是靠近點
是靠近點![]() 的四等分點,延長
的四等分點,延長![]() 交
交![]() 于點
于點![]() ,在梯形
,在梯形![]() 內,過
內,過![]() 作
作![]() 的平行線交
的平行線交![]() 于
于![]() ,則點
,則點![]() 即為所求,再由
即為所求,再由![]() ,即可確定點
,即可確定點![]() 的位置.
的位置.
(1)![]() 點
點![]() 在平面
在平面![]() 內的射影為
內的射影為![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又![]() 四邊形
四邊形![]() 是平行四邊形,
是平行四邊形,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,![]() ,
,
![]() 四邊形
四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
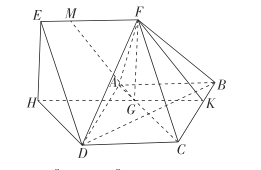
(2)假設在![]() 上是存在點
上是存在點![]() ,使
,使![]() 平面
平面![]() ,
,
![]() 四棱錐
四棱錐![]() 的體積為2,即
的體積為2,即![]() ,
,
![]() ,又
,又![]() ,
,![]() ,即點
,即點![]() 是靠近點
是靠近點![]() 的四等分點.
的四等分點.
延長![]() 交
交![]() 于點
于點![]() ,在梯形
,在梯形![]() 內,過
內,過![]() 作
作![]() 的平行線交
的平行線交![]() 于
于![]() ,
,
則點![]() 即為所求.
即為所求.
![]() ,即點
,即點![]() 是靠近點
是靠近點![]() 的四等分點.
的四等分點.


科目:高中數學 來源: 題型:
【題目】設![]() 是定義在R上的兩個周期函數,
是定義在R上的兩個周期函數,![]() 的周期為4,
的周期為4,![]() 的周期為2,且
的周期為2,且![]() 是奇函數.當
是奇函數.當![]() 時,
時,![]() ,
, ,其中k>0.若在區間(0,9]上,關于x的方程
,其中k>0.若在區間(0,9]上,關于x的方程![]() 有8個不同的實數根,則k的取值范圍是_____.
有8個不同的實數根,則k的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,有下述命題:①若
,有下述命題:①若![]() 是奇函數,則
是奇函數,則![]() 的圖象關于點
的圖象關于點![]() 對稱;②函數
對稱;②函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱,則
對稱,則![]() 為偶函數;③若對
為偶函數;③若對![]() ,有
,有![]() ,則2是
,則2是![]() 的一個周期;④函數
的一個周期;④函數![]() 與
與![]() 的圖象關于直線
的圖象關于直線![]() 對稱.其中正確的命題是______.(寫出所有正確命題的序號)
對稱.其中正確的命題是______.(寫出所有正確命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁和戊5名學生進行某種勞動技術比賽,決出了第1到第5名的名次.甲乙兩名參賽者去詢問成績,回答者對甲說,“很遺憾,你和乙都沒沒有拿到冠軍.”對乙說,“你當然不會是最差的.”從這個回答分析,甲是第五名的概率是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1為某省2018年1~4月快遞業務量統計圖,圖2是該省2018年1~4月快遞業務收入統計圖,下列對統計圖理解錯誤的是( )


A. 2018年1~4月的業務量,3月最高,2月最低,差值接近2000萬件
B. 2018年1~4月的業務量同比增長率均超過50%,在3月底最高
C. 從兩圖來看,2018年1~4月中的同一個月的快遞業務量與收入的同比增長率并不完全一致
D. 從1~4月來看,該省在2018年快遞業務收入同比增長率逐月增長
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com