【題目】已知數列
前
項和為
，且
，若
，則首項
的取值范圍是______.
【答案】
【解析】
根據
和
，化簡得到
，用該遞推關系，得到
，兩式相減，得
，可得數列
是從第二項開始的偶數項，組成的以4為公差的等差數列，由，可得
，可得是從第三項開始的奇數項，組成的以4為公差的等差數列，再利用
，得出
，用
依次表示出
，
，
，
，
，
，然后，根據
，即可求出首項的取值范圍
，
，
兩式相減，
，化簡得，①
進而可以利用該遞推關系，得到，②
然后
得，
，化簡得，可得數列是從第二項開始的偶數項，組成的以4為公差的等差數列，由，可得，可得是從第三項開始的奇數項，組成的以4為公差的等差數列，
又，則有
，
，
，
，
，對
，，則
由
，從第二項開始，得
由
得，
，
由
得，
，
由
得，，
由
得，，
，明顯地，解得
綜上，的取值范圍是
故正確答案為：
科目：高中數學 來源： 題型：
【題目】雙紐線最早于1694年被瑞士數學家雅各布·伯努利用來描述他所發(fā)現(xiàn)的曲線.在平面直角坐標系
中，把到定點
，
距離之積等于
的點的軌跡稱為雙紐線
.已知點
是雙紐線上一點，下列說法中正確的有（ ）
①雙紐線經過原點
； ②雙紐線關于原點中心對稱；
③
； ④雙紐線上滿足
的點
有兩個.
A.①②B.①②③C.②③D.②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（1）當a=-2時，求函數f(x)的極值；
（2）若ln[e(x+1)]≥2- f(-x)對任意的x∈[0，+∞)成立，求實數a的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數學中有許多形狀優(yōu)美、寓意美好的曲線，曲線C：
就是其中之一（如圖）.給出下列三個結論：
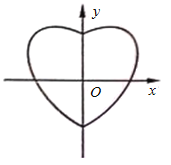
①曲線C恰好經過6個整點（即橫、縱坐標均為整數的點）；
②曲線C上任意一點到原點的距離都不超過
；
③曲線C所圍成的“心形”區(qū)域的面積小于3.
其中，所有正確結論的序號是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
（
為參數）.以坐標原點為極點，
軸的非負半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）將的方程化為普通方程，將的方程化為直角坐標方程；
（2）已知直線
的參數方程為
（
，
為參數，且
），與交于點
，與交于點
，且
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
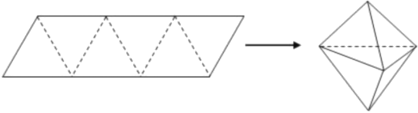
【題目】農歷五月初五是端午節(jié)，民間有吃粽子的習慣，粽子又稱粽粒，俗稱“粽子”，古稱“角黍”，是端午節(jié)大家都會品嘗的食品，傳說這是為了紀念戰(zhàn)國時期楚國大臣、愛國主義詩人屈原．如圖，平行四邊形形狀的紙片是由六個邊長為2的正三角形構成的，將它沿虛線折起來，可以得到如圖所示粽子形狀的六面體，則該六面體的表面積為________；該六面體內有一球，則該球體積的最大值為________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2020年春節(jié)突如其來的新型冠狀病毒肺炎在湖北爆發(fā)，一方有難八方支援，全國各地的白衣天使走上戰(zhàn)場的第一線，某醫(yī)院抽調甲、乙兩名醫(yī)生，抽調
、
、
三名護士支援武漢第一醫(yī)院與第二醫(yī)院，參加武漢疫情狙擊戰(zhàn)其中選一名護士與一名醫(yī)生去第一醫(yī)院，其它都在第二醫(yī)院工作，則醫(yī)生甲和護士被選在第一醫(yī)院工作的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
